Pourquoi les bulles de savon sont elles sphériques ?

Introduction

Quand on souffle dans un anneau trempé de savon, une bulle apparaît… et elle est presque toujours sphérique. Pourtant, on pourrait imaginer des bulles cubiques, pyramidales…

Ce phénomène cache en fait des mathématiques (comme toujours 🙂)

I. L’inégalité isopérimétrique

Une bulle de savon est un mince film d’eau maintenu par une couche de molécules de savon (cf. schéma ci-dessous).

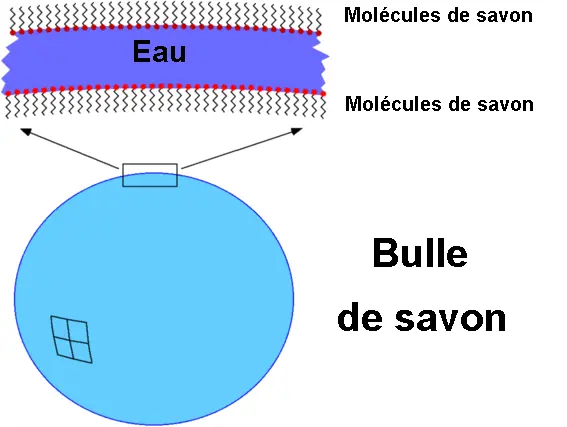
Mais pourquoi est-elle toujours sphérique (ou presque) ?

Tout commence avec une idée mathématique ancienne : l’inégalité isopérimétrique. Elle cherche à répondre à la question suivante : quelle est la plus grande surface qu’on peut délimiter à partir d’un périmètre donné ?

1. Anecdote historique

Didon était une princesse phénicienne. Son frère, le roi Pygmalion, tua son mari pour s’emparer de ses richesses. Elle décida alors de fuir par la mer ⛵. En arrivant en Afrique, Didon demanda au roi Jarbas de Numidie de lui vendre un terrain pour s’installer avec son peuple.

Jarbas accepta, mais de manière mesquine : il lui proposa seulement autant de terre qu’elle pourrait entourer avec une peau de bœuf. Didon eut alors une idée ingénieuse 😏 : elle fit découper la peau en fines lanières, les attacha bout à bout pour former une longue corde, puis l’étendit au sol en cercle.

De cette façon, elle réussit à enfermer la plus grande surface possible avec un périmètre donné. C’est le fameux problème isopérimétrique : parmi toutes les courbes fermées de même longueur, c’est le cercle qui enferme la plus grande aire.

Grâce à cette ruse, Didon obtint un vaste terrain, où elle fonda la ville de Carthage.

Justement, la petite histoire que l’on vient de raconter illustre l’inégalité isopérimétrique (dans un contexte à 2 dimensions pour être plus précis).

Pour le Grand Oral, je trouve que cela peut être une bonne idée de démarrer avec une petite histoire, comme celle-ci. Cela permet de capter l’attention du jury dès le début et de rendre l’exposé plus vivant.

2. Cas concrets: dimensions 2 et 3

En dimension 2, on a l’inégalité suivante :

S \leq \frac{P^2}{4\pi}

où [math] S [/math] est l’aire et [math] P [/math] le périmètre.

C’est une inégalité qui est toujours vraie, donc si on fixe la valeur du périmètre, on a une majoration de l’aire, et si on fixe l’aire on a une minoration du périmètre.

Pour un disque de rayon [math] R [/math], on a [math] S = \pi R^2 [/math] et [math] P = 2\pi R [/math], donc si l’on remplace ces valeurs dans l’inégalité précédente, on voit bien que cela devient une égalité puisque : [math] \pi R^2 = \frac{(2\pi R)^2}{4\pi} [/math].

L’inégalité devient une égalité. On dit que le disque est optimal (concrètement cela veut dire que le disque représente le meilleur cas possible), comme on l’a vu avec l’histoire de Didon.

En dimension 3, l’inégalité devient :

V^2 \leq \frac{S^3}{36\pi}

où [math] V [/math] est le volume et [math] S [/math] la surface.

Pour une sphère de rayon [math] R [/math] : [math] V = \frac{4}{3}\pi R^3, S = 4\pi R^2 [/math]. On obtient de nouveau une égalité. Autrement dit, la sphère est la forme optimale : toute autre surface de même aire contient un volume plus petit.

II. Minimiser la surface, une question d’énergie

1. Pourquoi les molécules de surface coûtent plus d’énergie ?

Imaginons une goutte d’eau : les molécules à l’intérieur sont attirées dans toutes les directions → les forces s’équilibrent. Mais celles qui sont à la surface n’ont pas de voisines vers l’extérieur : elles sont donc attirées vers l’intérieur seulement.

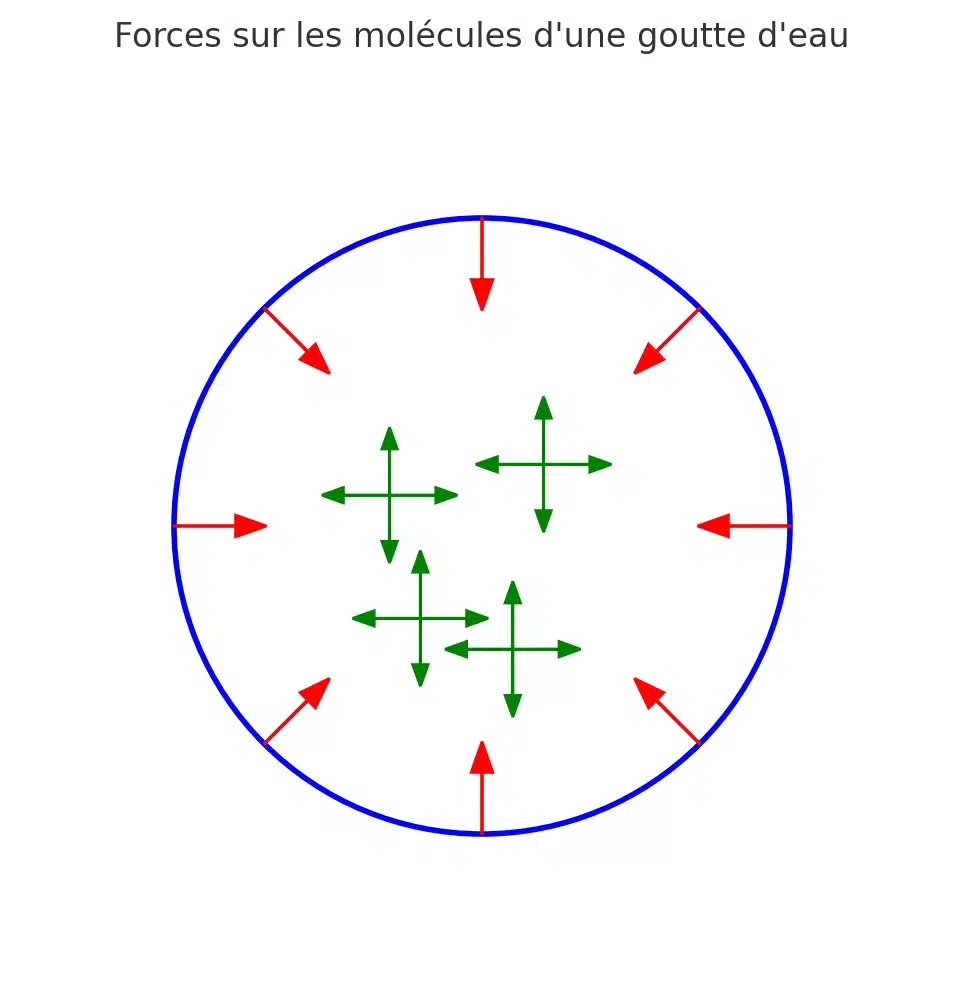
On appelle cela la tension superficielle.

On sait même que l’énergie de surface est proportionnelle à l’aire :

E = \gamma \times A

où [math] \gamma [/math] est la tension superficielle.

Ainsi, de ce rappel on déduit que la bulle va chercher à réduire son aire (puisque, d’après la formule précédente, cela revient à réduire son énergie étant donné que les deux sont proportionnels).

(Petit aparté sur la tension superficielle : c’est la même raison pour laquelle l’eau peut dépasser légèrement le bord d’un verre sans déborder, la tension de surface la maintient 😮)

2. Pourquoi la sphère est la meilleure candidate ?

La goutte (et donc la bulle) cherche à réduire son aire. Mais comme les liquides sont incompressibles, elle doit garder le même volume.

Le problème devient donc purement mathématique : parmi toutes les formes de volume fixé, laquelle minimise l’aire ?

C’est le théorème isopérimétrique qui répond : la sphère :).

En effet, pour une sphère de rayon [math] R [/math] :

V = \tfrac{4}{3}\pi R^3, A = 4\pi R^2

Et pour toute autre forme ayant le même volume, l’aire est forcément plus grande.

On comprend donc maintenant mieux pourquoi les bulles sont sphériques.

III. La loi de Laplace et la stabilité des bulles

1. Pression et courbure

On a donc compris pourquoi la bulle adopte une forme sphérique : c’est celle qui minimise l’aire pour un volume donné. Mais une bulle de savon, ce n’est pas seulement de la géométrie : il y a aussi des phénomènes physiques qui entrent en jeu. Pour bien comprendre sa stabilité, il faut parler de la loi de Laplace.

Reprenons une analogie : un ballon de baudruche. Plus on souffle dedans, plus sa paroi se tend. De même, une bulle de savon subit une surpression interne due à la courbure de sa surface.

La loi de Laplace nous donne la formule :

\Delta p = \frac{2\gamma}{R}

où :

• [math] \Delta p [/math] = différence de pression intérieur/extérieur,
• [math] \gamma [/math] = tension de surface,
• [math] R [/math] = rayon de la bulle.

Si deux bulles de tailles différentes communiquent, l’air s’écoule naturellement de la petite (forte pression) vers la grande (faible pression). Peu à peu, la petite bulle disparaît et la grande grossit.

2. Cas particulier des bulles de savon

Attention, une bulle de savon n’est pas une simple goutte : c’est une fine lame d’eau entourée d’air, donc il y a deux interfaces (air/eau à l’extérieur et à l’intérieur).

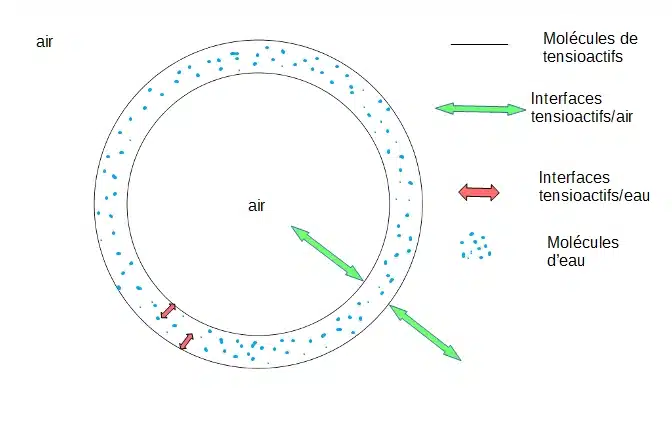
La loi de Laplace se modifie légèrement :

\Delta p = \frac{4\gamma}{R}

Ce qui rend les petites bulles encore plus instables. C’est pourquoi, en pratique, quand plusieurs bulles se rejoignent, elles s’organisent ou disparaissent de façon à minimiser la surface totale.

Voici une vidéo super courte pour bien visualiser tout ça :

Conclusion

Les bulles de savon sont donc sphériques parce que :

• L’inégalité isopérimétrique montre que la sphère est la forme optimale qui maximise le volume pour une surface donnée.
• La tension de surface pousse la bulle à minimiser son énergie → donc sa surface.

La sphère n’est donc pas un hasard esthétique !

D’ailleurs, si une bulle prend une autre forme (par exemple collée à une paroi), dès que ces contraintes disparaissent, elle redevient sphérique.

Si vous voulez creuser la partie physique, n’hésitez pas à aller voir cette page.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve ! N’hésitez pas à laisser un commentaire ci-dessous si vous avez la moindre question ou remarque. Bon courage 💪