Le Nombre d’Or et la Suite de Fibonacci

Introduction

Depuis l’Antiquité, un nombre fascine aussi bien les mathématiciens que les artistes : le nombre d’or [math]\varphi \approx 1,618[/math]. On le retrouve dans l’architecture grecque 🏛️, dans les peintures de Léonard de Vinci, dans les spirales de coquillages ou même dans les proportions des tournesols.

Mais derrière ce mythe « esthétique », il y a surtout des mathématiques… (quand on vous dit qu’on les retrouve partout !)

Problématique : Comment le nombre d’or relie-t-il algèbre, suites et géométrie, et pourquoi apparaît-il si souvent dans la nature et les constructions humaines ?

I. Définition et propriétés algébriques

1. Équation du nombre d’or

Le nombre d’or apparaît d’abord dans un problème de proportion. On cherche un rapport [math]\varphi[/math] tel que, pour un segment coupé en deux parties [math]a[/math] et [math]b[/math], la proportion soit la même à deux niveaux :

\frac{a+b}{a} = \frac{a}{b}

Autrement dit, le rapport entre le tout et la grande partie est égal au rapport entre la grande et la petite partie.

Si l’on note [math]\varphi = \frac{a}{b}[/math], cette équation devient :

\varphi = 1 + \frac{1}{\varphi}

En multipliant les deux côtés par [math]\varphi[/math], on obtient une équation quadratique :

\varphi^2 = \varphi + 1

C’est une équation du second degré, que l’on peut résoudre avec la formule classique :

\varphi = \frac{1 \pm \sqrt{5}}{2}

Comme [math]\varphi[/math] est un rapport de longueurs positif, on garde la racine positive :

\varphi = \frac{1+\sqrt{5}}{2} \approx 1,618

2. Propriétés remarquables

Le nombre d’or a des propriétés étonnantes, faciles à démontrer :

Son inverse est très simple :

\frac{1}{\varphi} = \varphi - 1 \approx 0,618.

Autrement dit, [math]\varphi[/math] et son inverse ne diffèrent que d’une unité.

Identité avec Fibonacci :

\varphi^n = F_n \varphi + F_{n-1},

où [math]F_n[/math] désigne le n-ième terme de la suite de Fibonacci ([math]1,1,2,3,5,8,13,\dots[/math]).

Cette identité relie directement un nombre « géométrique » (le nombre d’or) à une suite « arithmétique ».

Par exemple, calculons [math]\varphi^3[/math]. Comme [math]\varphi^2 = \varphi + 1[/math], on a :

\varphi^3 = \varphi \cdot \varphi^2 = \varphi (\varphi+1) = \varphi^2 + \varphi = 2\varphi + 1 \approx 4,236.

II. Suites et convergence vers le nombre d’or

1. Suite de Fibonacci

Comme nous venons de le voir, le nombre d’or a un lien direct avec la célèbre suite de Fibonacci (suite qu’on ne présente plus normalement, à connaître).

La suite est définie par récurrence :

u_0 = 0, u_1 = 1, u_{n+2} = u_{n+1} + u_n

Autrement dit, chaque terme est la somme des deux précédents : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

Si l’on calcule le rapport [math]\tfrac{u_{n+1}}{u_n}[/math] :

• [math]\tfrac{3}{2} = 1,5[/math]
• [math]\tfrac{5}{3} \approx 1,66[/math]
• [math]\tfrac{21}{13} \approx 1,615[/math]

On constate que ces quotients se rapprochent progressivement du nombre d’or [math]\varphi \approx 1,618[/math].

2. Formule de Binet

On peut montrer (avec une méthode hors programme) que la suite de Fibonacci admet une formule explicite : c’est la formule de Binet.

u_n = \frac{\varphi^n - (1-\varphi)^n}{\sqrt{5}}

Ce qui nous intéresse ici, c’est la limite des rapports [math]\tfrac{u_{n+1}}{u_n}[/math].

On remarque que [math]|1-\varphi| < 1[/math]. Donc la puissance [math](1-\varphi)^n[/math] tend vers 0 quand [math]n[/math] devient grand.

Ainsi, pour [math]n[/math] grand :

u_n \approx \frac{\varphi^n}{\sqrt{5}}

et

\frac{u_{n+1}}{u_n} \approx \frac{\varphi^{n+1}/\sqrt{5}}{\varphi^n/\sqrt{5}} = \varphi.

III. Applications géométriques et trigonométriques

1. Pentagone régulier et diagonales d’or

Le nombre d’or apparaît naturellement dans la géométrie du pentagone régulier.

Dans un pentagone, si l’on trace toutes les diagonales, on obtient une étoile à 5 branches (le pentagramme).

On peut alors remarquer que le rapport entre la longueur d’une diagonale et celle d’un côté est exactement [math]\varphi[/math] (par exemple [math]\frac{AC}{AB} = \varphi[/math]).

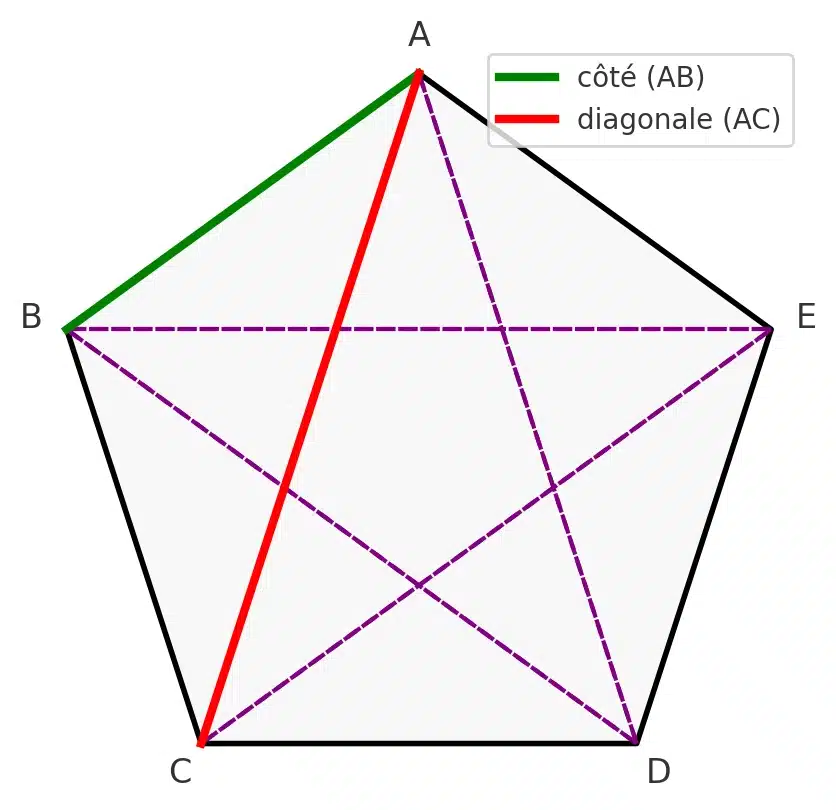
On peut même relier le pentagone régulier et le nombre d’or grâce à la trigonométrie.

Dans un pentagone, les angles au centre et aux sommets conduisent naturellement à des mesures de 36° et 72°.

Or, en étudiant les triangles isocèles formés par les diagonales et les côtés, on arrive à la relation :

\cos(36^\circ) = \tfrac{\varphi}{2}

C’est une identité étonnante : elle montre que la valeur trigonométrique d’un angle « simple » (36°) n’est pas un nombre décimal quelconque, mais qu’elle est directement liée au nombre d’or.

2. Spirale d’or et rectangles d’or

Un autre lieu où l’on retrouve le nombre d’or est la spirale d’or, très connue en art et en nature.

On commence par construire un rectangle d’or : c’est un rectangle dont le rapport longueur/largeur est [math]\varphi[/math].

Si l’on enlève un carré, il reste encore un rectangle d’or, plus petit.

En répétant ce procédé, on obtient une suite de rectangles de plus en plus petits.

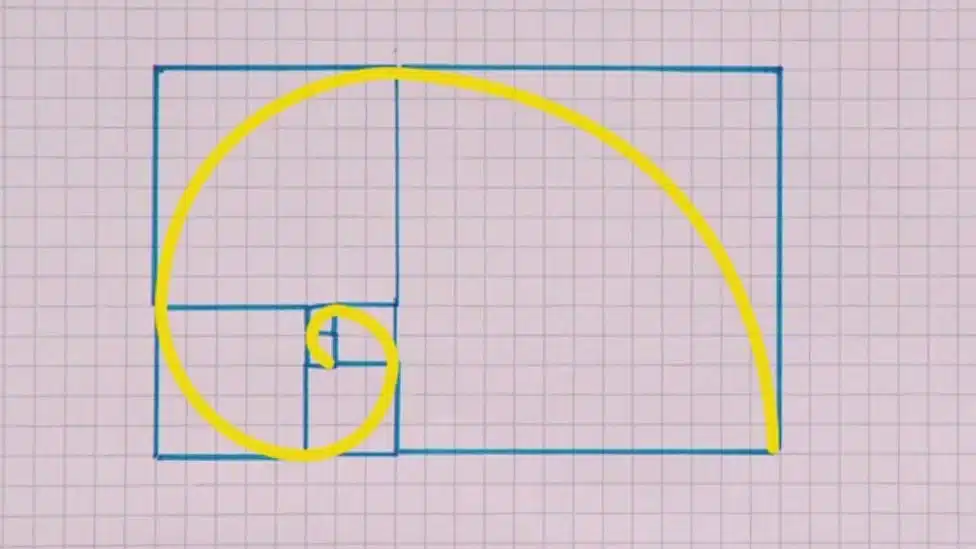
En reliant les coins de ces carrés par des quarts de cercle, on trace une spirale qui se rapproche d’une spirale logarithmique.

Voici une petite vidéo à visionner pour bien comprendre la construction étape par étape.

L’équation polaire de cette spirale est :

r = ae^{b\theta}

où [math]a[/math] et [math]b[/math] sont des constantes qui dépendent de la construction.

Cette spirale rappelle les formes que l’on observe dans la nature : coquilles de mollusques, cornes d’animaux, ou encore la disposition des graines dans un tournesol 🌻.

Conclusion

• Le nombre d’or [math]\varphi[/math] se résout avec une simple équation quadratique.
• On le retrouve comme limite des rapports de Fibonacci, grâce aux suites et à la formule de Binet.
• Il apparaît en géométrie, dans la nature…

Le nombre d’or, c’est finalement le symbole de ce que sont les mathématiques : un langage universel qui relie presque tout 🙂

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !