Une lunette astronomique permet-elle de voir un homme marcher sur la lune ?

Introduction

« Une lunette astronomique permet-elle vraiment de voir un homme marcher sur la Lune ? » La question peut sembler naïve, mais elle cache en réalité des mathématiques très intéressantes. 🌙🔭

Pour y répondre, il faut combiner plusieurs notions du programme : angles en radians, rapports de grandeurs, mais aussi des formules issues de l’optique ondulatoire comme le pouvoir séparateur. Autrement dit, c’est un problème où l’on confronte les ordres de grandeur aux limites physiques des instruments.

I. Taille apparente de l’homme vu depuis la Terre

1. Calcul de l’angle sous-tendu

L’angle sous-tendu (ou angle apparent) d’un objet, c’est l’angle qu’il occupe dans notre champ de vision.

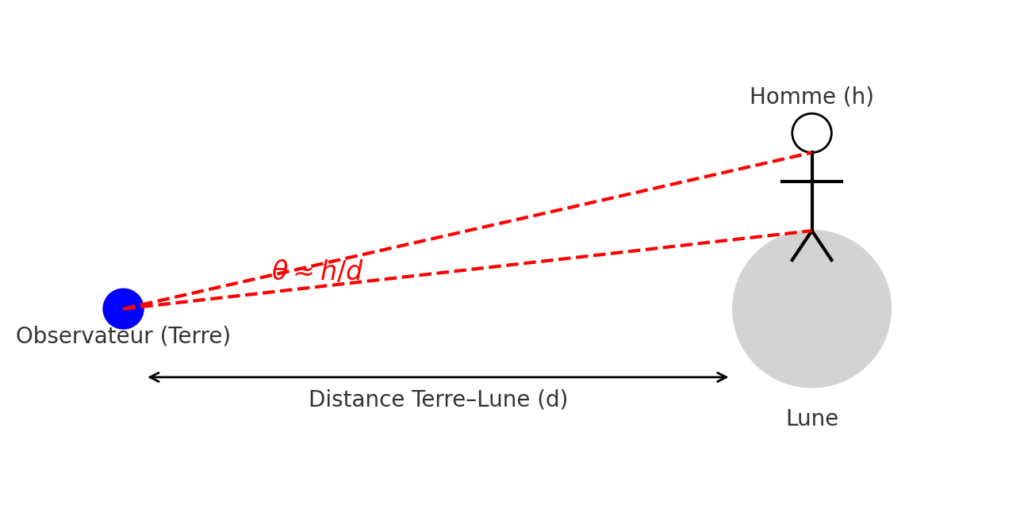
On utilise la formule d’angle sous-tendu (valable pour de petits angles) :

\theta \approx \tfrac{h}{d}.

• Taille d’un homme : [math]h \approx 1,8 \text{ m}[/math]
• Distance Terre–Lune : [math]d \approx 3,84 \times 10^8 \text{ m}[/math]

\theta \approx \tfrac{1,8}{3,84 \times 10^8} \approx 4,7 \times 10^{-9} \text{ rad}.

Conversion en secondes d’arc (1 rad = 206 265 arcsec) :

\theta \approx 4,7 \times 10^{-9} \times 206,265 \approx 10^{-3} \text{ arcsec}.

2. Comparaison avec la taille apparente de la Lune

• Diamètre de la Lune : [math]D = 3,474 \times 10^6 \text{ m}[/math]
• Distance : [math]d = 3,84 \times 10^8 \text{ m}[/math]

\theta_{\text{Lune}} \approx \tfrac{D}{d} = \tfrac{3,474 \times 10^6}{3,84 \times 10^8} \approx 9,0 \times 10^{-3}  \text{ rad}

En degrés : [math]\theta_{\text{Lune}} \approx 0,52^\circ \approx 1800 \text{ arcsec}[/math]

Comparons :

• Lune : [math]1800 \text{ arcsec}[/math]
• Homme : [math]0,001 \text{ arcsec}[/math]

Rapport :

\tfrac{1800}{0,001} = 1,8 \times 10^6.

Un homme sur la Lune apparaît donc 1,8 million de fois plus petit que la Lune vue dans le ciel.

II. Résolution d’une lunette astronomique

1. Pouvoir séparateur (formule de Rayleigh)

Le pouvoir séparateur d’une lunette dépend de la diffraction de la lumière. La formule de Rayleigh donne :

\theta = 1,22 \cdot \tfrac{\lambda}{D}.

• Longueur d’onde moyenne de la lumière visible : [math]\lambda \approx 550 \text{ nm} = 5,5 \times 10^{-7} \text{ m}[/math]
• Diamètre d’un objectif amateur : [math]D = 10 \text{ cm} = 0,10 \text{ m}[/math]

\theta = 1,22 \cdot \tfrac{5,5 \times 10^{-7}}{0,10} \approx 6,7 \times 10^{-6} \text{ rad}.

Conversion en secondes d’arc :

\theta \approx 6,7 \times 10^{-6} \times 206,265 \approx 1,4 \text{ arcsec}.

Or, l’homme sur la Lune correspond à [math]10^{-3} \text{ arcsec}[/math].

C’est plus de mille fois trop petit → une lunette amateur ne peut absolument pas le voir.

2. Taille théorique nécessaire

On peut chercher le diamètre [math]D[/math] qu’il faudrait pour atteindre un pouvoir séparateur suffisant :

D \geq 1,22 \cdot \tfrac{\lambda}{\theta}

Avec :

• [math]\lambda = 5,5 \times 10^{-7} \text{ m}[/math]
• [math]\theta = 10^{-3} \text{ arcsec} = \tfrac{10^{-3}}{206,265} \text{ rad} \approx 4,8 \times 10^{-9} \text{ rad}[/math]

D \geq \tfrac{1,22 \cdot 5,5 \times 10^{-7}}{4,8 \times 10^{-9}} \approx 1,4 \times 10^{2} \text{ m}.

Il faudrait donc un objectif d’environ 140 mètres de diamètre (l’équivalent d’un stade de football !) pour distinguer un homme sur la Lune.

III. Grossissement et limites pratiques

1. Grossissement d’une lunette

Le grossissement d’une lunette (combien l’image paraît « plus grande ») dépend de la focale de l’objectif et de l’oculaire :

G = \tfrac{f_{\text{objectif}}}{f_{\text{oculaire}}}.

Problème : grossir une image floue… donne une image floue, juste plus grande. La limite réelle vient du pouvoir séparateur (diffraction + turbulence), pas du grossissement.

Même avec un très fort grossissement, par exemple [math]G=1000[/math], l’angle apparent de l’homme sur la Lune reste fixé par la résolution : l’homme correspond à [math]\approx 10^{-3} \text{ arcsec}[/math], alors qu’une lunette de 10 cm sépare au mieux [math]\approx 1{,}4 \text{ arcsec}[/math] (voir partie II).

2. Comparaison avec des télescopes modernes

Prenons un instrument emblématique : le télescope spatial Hubble, de diamètre [math]D=2{,}4 \text{ m}[/math].

Sa limite de diffraction à [math]\lambda\approx 550 \text{ nm}[/math] vaut (formule de Rayleigh) :

\theta \approx 1.22 \cdot \tfrac{\lambda}{D} 
\;\approx\; 1.22 \cdot \tfrac{5.5 \times 10^{-7}}{2.4} 
\;\approx\; 2.8 \times 10^{-7}\,\text{rad} 
\;\approx\; 0.06\,\text{arcsec}.

C’est excellent… mais encore 60 fois trop grand pour atteindre [math]10^{-3} \text{ arcsec}[/math].

Même Hubble ne pourrait pas distinguer un homme sur la Lune depuis l’orbite terrestre.

Conclusion pratique : aucune lunette/télescope terrestre (et même spatial de quelques mètres) ne peut y parvenir ; les meilleures images des traces humaines (modules, empreintes des rovers, etc.) sont obtenues par des sondes en orbite lunaire (à faible distance), pas par des instruments observant depuis la Terre.

Conclusion

• Le pouvoir séparateur des lunettes et télescopes est des centaines ou milliers de fois trop faible.
• Résultat : aucune lunette astronomique ne peut distinguer un homme sur la Lune, seules des sondes proches de la surface l’ont permis. 🚀

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !