Comment les mathématiques peuvent aider pour le traitement des cancers ?

Introduction

Le cancer fait peur parce qu’il touche énormément de personnes, mais on oublie souvent que derrière la médecine, il y a aussi… des mathématiques. Elles permettent de comprendre comment une tumeur grandit, de mesurer l’efficacité d’un traitement et même d’optimiser les doses de médicaments. L’idée est donc de voir comment les maths peuvent aider, concrètement, à mieux traiter les cancers.

I. Modéliser la croissance des cellules cancéreuses

1. Croissance exponentielle et logistique

La première idée, en mathématiques, est de modéliser la croissance d’une population de cellules comme une croissance exponentielle.

Si [math]N(t)[/math] désigne le nombre de cellules au temps [math]t[/math], alors on peut écrire :

N(t) = N_0 e^{rt}

où :

• [math]N_0[/math] est le nombre initial de cellules,
• [math]r[/math] est le taux de croissance (plus il est grand, plus la tumeur grossit vite).

Ce modèle correspond à une suite géométrique si l’on considère des pas de temps discrets (jour après jour).

Cependant, dans un organisme réel, cette croissance n’est pas illimitée : la tumeur finit par manquer d’espace, de nutriments ou être freinée par le système immunitaire. On utilise alors le modèle logistique :

N(t) = \dfrac{K}{1 + A e^{-rt}}

où :

• [math]K[/math] représente la capacité maximale (taille limite que la tumeur peut atteindre),
• [math]A[/math] dépend du nombre initial de cellules.

Contrairement à l’exponentielle, la courbe logistique commence par croître rapidement, puis se stabilise.

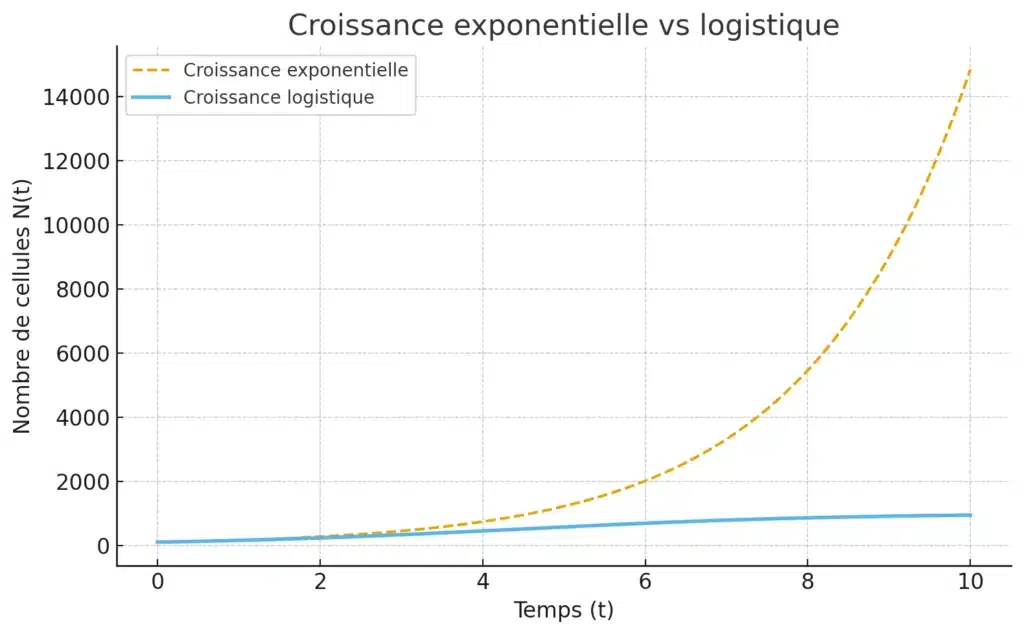
2. Intérêt médical de ces modèles

Ces modèles ont une véritable utilité médicale :

• Si le paramètre [math]r[/math] est grand, la tumeur est dite «agressive» → elle grossit très vite, et le traitement doit être mis en place rapidement.
• Si [math]r[/math] est petit, la croissance est plus lente → les médecins peuvent parfois observer l’évolution avant d’agir.

De plus, la forme logistique permet de mieux anticiper la taille future d’une tumeur et donc de décider du moment optimal pour intervenir.

II. Probabilités et statistiques : comprendre les traitements

1. Probabilité de survie et loi exponentielle

En médecine, on s’intéresse souvent à la durée de survie après un traitement.

On peut modéliser cette durée par une variable aléatoire [math]T[/math].

Un modèle simple est la loi exponentielle :

\mathbb{P}(T > t) = e^{-\lambda t}

Cela signifie que la probabilité qu’un patient survive plus de [math]t[/math] années diminue de façon exponentielle.

On peut calculer l’espérance de vie d’un patient dans ce modèle :

\mathbb{E}[T] = \dfrac{1}{\lambda}

Interprétation :

• si [math]\lambda[/math] est grand, la survie moyenne est courte → le traitement est peu efficace.
• si [math]\lambda[/math] est petit, la survie moyenne est longue → le traitement est plus efficace.

Ainsi, une simple formule mathématique permet de comparer l’impact de deux traitements différents sur l’espérance de vie.

Exemple numérique :

Supposons deux traitements différents :

• Traitement A : [math]\lambda = 0{,}2[/math]
  [math]\mathbb{E}[T] = \dfrac{1}{0{,}2} = 5[/math] ans en moyenne.
• Traitement B : [math]\lambda = 0{,}1[/math]
  [math]\mathbb{E}[T] = \dfrac{1}{0{,}1} = 10[/math] ans en moyenne.

Cela signifie que le traitement B double l’espérance de vie par rapport au traitement A (en moyenne évidemment, rien n’est sûr).

2. Statistiques et essais cliniques

Lorsqu’on teste un traitement, on observe un grand nombre de patients.

On peut alors modéliser la réussite d’un traitement (par exemple, une rémission) comme une épreuve de Bernoulli.

Si [math]n[/math] est le nombre total de patients, et [math]p[/math] la probabilité qu’un patient guérisse, alors le nombre de succès [math]X[/math] suit une loi binomiale :

X \sim \mathcal{B}(n,p)

On a :

• [math]\mathbb{E}[X] = np[/math] (le nombre moyen de patients en rémission),
• [math]\text{Var}(X) = np(1-p)[/math] (la variabilité des résultats).

Exemple : si un traitement a une probabilité de réussite de [math]p = 0{,}6[/math] sur [math]n = 100[/math] patients, alors on attend en moyenne [math]60[/math] rémissions, mais ce nombre peut varier autour de cette valeur.

Ces outils permettent de comparer deux traitements :

• par exemple, une chimiothérapie avec [math]p = 0{,}6[/math],
• contre une immunothérapie avec [math]p = 0{,}75[/math].

Même si on ne peut pas prédire le sort de chaque patient, on peut conclure mathématiquement que le second traitement est globalement plus efficace.

III. Optimiser les doses et les stratégies de traitement

1. Modèle mathématique des doses

Lorsqu’un médicament est injecté dans le corps, sa concentration dans le sang ne reste pas constante : elle diminue progressivement avec le temps.

Un modèle simple est la décroissance exponentielle :

C(t) = C_0 e^{-\lambda t}

où :

• [math]C_0[/math] est la concentration initiale,
• [math]\lambda[/math] mesure la vitesse d’élimination du médicament.

Cela explique pourquoi il faut répéter les injections.

Si l’on administre une dose à intervalles réguliers, on peut modéliser la concentration totale comme une suite géométrique : chaque nouvelle injection rajoute [math]C_0[/math], puis cette contribution décroît comme [math]e^{-\lambda t}[/math].

Ainsi, pour que le traitement soit efficace, il faut choisir un intervalle de temps entre deux doses qui maintienne la concentration [math]C(t)[/math] au-dessus d’un certain seuil thérapeutique.

2. Mathématiques de l’optimisation

Le problème médical est de trouver un équilibre :

• si la dose est trop faible → inefficacité, les cellules cancéreuses ne sont pas détruites,
• si la dose est trop forte → toxicité, les cellules saines sont également touchées.

On peut traduire cette idée avec une fonction mathématique qui mesure l’efficacité du traitement.

Par exemple :

f(x) = ax - bx^2

où :

• [math]x[/math] est la dose,
• le terme [math]ax[/math] correspond au bénéfice (plus la dose est grande, plus le traitement agit),
• le terme [math]-bx^2[/math] représente les effets secondaires qui augmentent rapidement avec la dose.

Cette fonction a une forme de parabole. On peut montrer que son maximum est atteint pour :

x = \dfrac{a}{2b}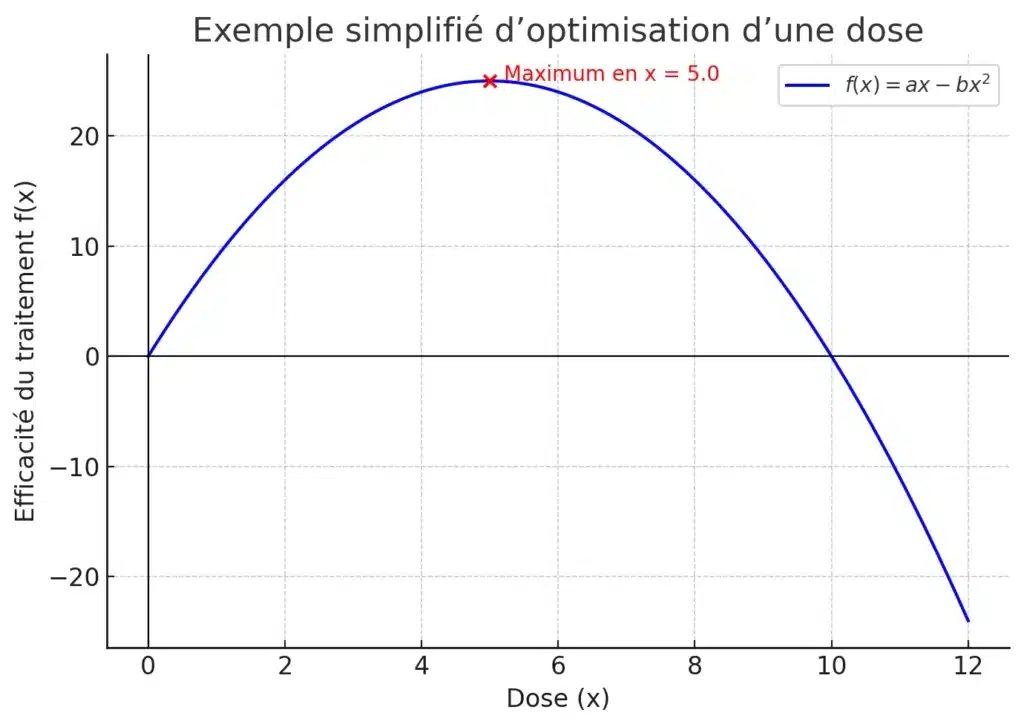

Ce petit calcul, même s’il repose sur une fonction simplifiée, illustre bien l’idée d’optimisation : en pratique, les médecins utilisent des modèles plus complexes, mais on comprend ici le principe qui consiste à chercher la dose qui maximise l’efficacité tout en limitant les effets indésirables.

Conclusion

Les mathématiques ne remplacent pas la médecine, mais elles donnent des outils pour modéliser, prévoir et optimiser les traitements. Elles transforment des phénomènes biologiques complexes en équations qu’on peut analyser, et permettent ainsi d’améliorer la prise en charge des cancers. C’est une belle preuve que les maths peuvent, d’une certaine manière, contribuer à sauver des vies.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !