Approximation de Pi

Introduction

On a tous déjà entendu parler de [math]\pi[/math], ce nombre mystérieux qui relie le cercle à son diamètre. Mais comme il a une infinité de décimales, les mathématiciens ont dû inventer plein de façons de l’approcher…

I. π : définitions et premières approximations

1. Définition géométrique et historique

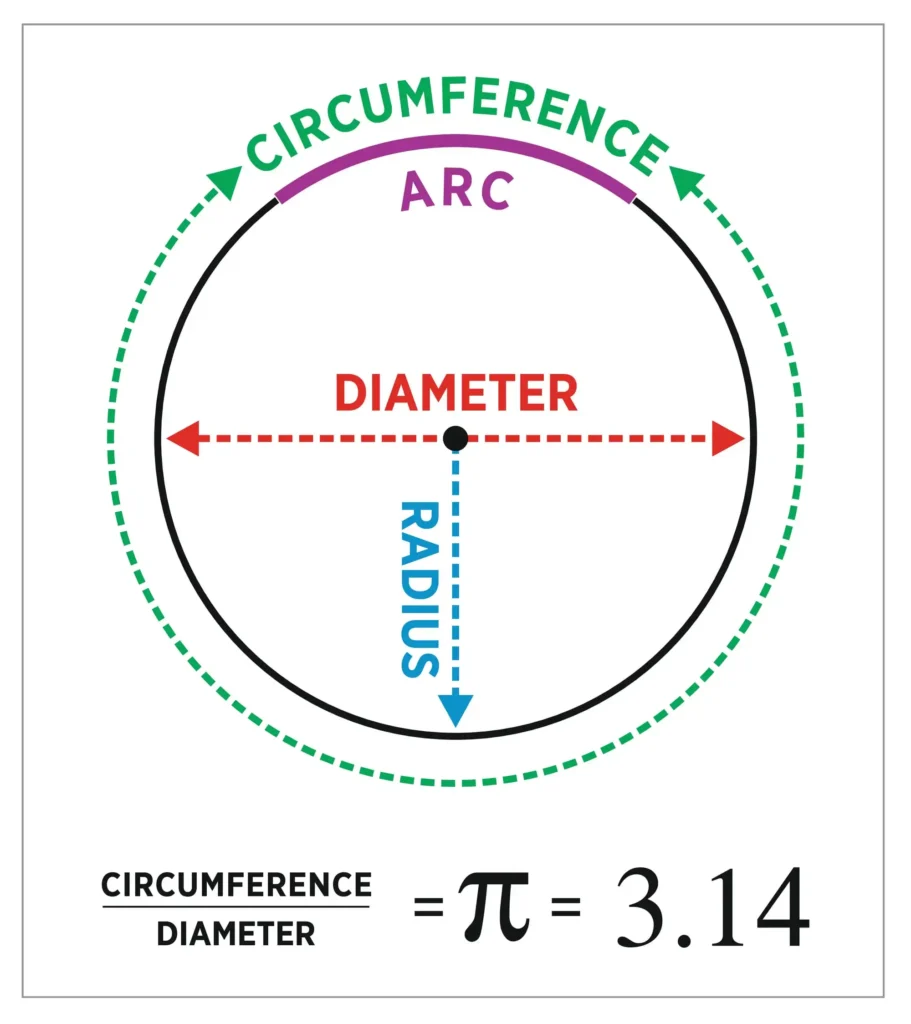
Le nombre [math]\pi[/math] est défini comme le rapport entre la circonférence d’un cercle et son diamètre :

\pi = \dfrac{\text{périmètre du cercle}}{\text{diamètre}}.

Ce rapport est le même pour tous les cercles, petits ou grands, et c’est ce qui en fait une constante universelle.

Depuis l’Antiquité, les civilisations ont essayé d’approcher [math]\pi[/math] :

• En Égypte, le papyrus Rhind (~-1650) donne [math]\pi \approx 3,16[/math].
• Archimède (-287 à -212) propose une méthode géométrique ingénieuse : il encadre le cercle par des polygones réguliers inscrits et circonscrits, puis calcule leur périmètre. En augmentant le nombre de côtés, on se rapproche de la circonférence du cercle. Résultat : il obtient [math]3,1408 < \pi < 3,1429[/math], une précision remarquable pour l’époque.

Mathématiquement, cette méthode consiste à créer une suite d’approximation : à mesure que le nombre de côtés augmente, la valeur trouvée converge vers [math]\pi[/math].

2. Propriétés et nature de [math]\pi[/math]

Au fil des siècles, les mathématiciens ont découvert des propriétés fondamentales de [math]\pi[/math] :

• En 1761, Lambert démontre que [math]\pi[/math] est irrationnel : il ne peut pas s’écrire comme une fraction [math]\tfrac{p}{q}[/math] d’entiers.
• En 1882, Lindemann prouve que [math]\pi[/math] est même transcendant : il n’est solution d’aucune équation polynomiale à coefficients entiers.

Ainsi, il est impossible de déterminer [math]\pi[/math] avec une fraction ou même une équation polynomiale.

La seule manière de l’approcher est donc d’utiliser :

• des séries infinies (comme la série de Leibniz ou de Machin),
• des fractions continues qui donnent de très bonnes approximations,
• ou des méthodes géométriques/probabilistes.

II. Méthodes mathématiques pour approximer [math]\pi[/math]

1. Approches géométriques et analytiques

À partir du XVIIe siècle, les mathématiciens trouvent des formules analytiques permettant de calculer [math]\pi[/math] directement à partir de séries infinies.

Exemple célèbre : la série de Leibniz :

\pi = 4\sum_{k=0}^{\infty} \frac{(-1)^k}{2k+1} = 4\left(1 - \tfrac{1}{3} + \tfrac{1}{5} - \tfrac{1}{7} + \dots \right).

Cette série est exacte mais converge très lentement : pour obtenir seulement 2 décimales correctes, il faut déjà plusieurs centaines de termes.

Pour gagner en efficacité, on utilise des identités trigonométriques comme celle de Machin (1706) :

\pi = 16\arctan\tfrac{1}{5} - 4\arctan\tfrac{1}{239}.

Ces formules, basées sur le développement en série de [math]\arctan(x)[/math], ont permis de calculer [math]\pi[/math] à des centaines de décimales, bien avant l’invention des ordinateurs.

2. Approches probabilistes : la méthode Monte-Carlo

Au XVIIIe siècle, le mathématicien Buffon imagine une expérience aléatoire : le lancer d’aiguille. En analysant la probabilité que l’aiguille coupe une ligne tracée sur le sol, on peut retrouver une approximation de [math]\pi[/math].

Aujourd’hui, une méthode plus simple et populaire est celle du disque inscrit :

• On considère un carré de côté 2, centré à l’origine, dans lequel on inscrit un cercle de rayon 1.
• On tire au hasard un grand nombre de points dans le carré.
• La proportion de points qui tombent dans le cercle est proche de [math]\pi/4[/math].

Mathématiquement :

\dfrac{\text{aire du cercle}}{\text{aire du carré}} = \dfrac{\pi \cdot 1^2}{4} = \tfrac{\pi}{4}.

Donc :

\pi \approx 4 \times \dfrac{\text{points dans le cercle}}{\text{points totaux}}.

Grâce à la loi des grands nombres, plus on génère de points, plus l’approximation devient précise.

III. Implémentations numériques (NSI)

1. Simulation Monte-Carlo en Python

L’idée probabiliste du disque inscrit se prête très bien à une simulation informatique.

On peut écrire un programme Python qui génère des points aléatoires et compte combien tombent à l’intérieur du cercle unité.

Exemple de code :

import random

def approx_pi(n):
    inside = 0
    for _ in range(n):
        x, y = random.random(), random.random()  # point aléatoire dans le carré [0,1]×[0,1]
        if x**2 + y**2 <= 1:  # le point est dans le quart de disque
            inside += 1
    return 4 * inside / n   # proportion × 4 ≈ pi

print(approx_pi(100000))

Avec 100 000 points, on obtient une approximation autour de 3,14.

• Si on augmente le nombre d’essais, la valeur se rapproche de [math]\pi[/math].
• C’est une illustration de la loi des grands nombres : plus on simule, plus la moyenne des résultats converge vers la vraie valeur.

Cependant, la précision augmente lentement : pour gagner une décimale fiable, il faut multiplier le nombre d’essais par environ 100.

2. Comparaison avec d’autres méthodes numériques

On peut aussi coder d’autres formules d’approximation dans Python :

• Série de Leibniz :

def leibniz_pi(n):
    pi = 0
    for k in range(n):
        pi += (-1)**k / (2*k+1)
    return 4*pi

Problème : il faut plusieurs millions de termes pour avoir seulement 5 décimales correctes.

• Formule de Machin (avec math.atan) :

import math

pi_machin = 16*math.atan(1/5) - 4*math.atan(1/239)
print(pi_machin)

Cette méthode donne directement [math]\pi[/math] avec une grande précision, beaucoup plus rapidement.

3. Discussion : efficacité algorithmique

Ces comparaisons permettent de réfléchir à l’efficacité des algorithmes :

• certaines méthodes convergent très lentement (Leibniz, Monte-Carlo),
• d’autres donnent de bons résultats presque immédiatement (Machin, ou des formules modernes encore plus rapides).

En NSI, on peut visualiser la vitesse de convergence avec un graphe :

• en abscisse : le nombre d’itérations,
• en ordonnée : l’erreur par rapport à la vraie valeur de [math]\pi[/math].

Ainsi, le choix de l’algorithme compte autant que la puissance de calcul.

Conclusion

Finalement, même si on ne connaîtra jamais toutes ses décimales, [math]\pi[/math] reste un bel exemple de la créativité des mathématiciens : géométrie, probabilités et informatique se rejoignent pour l’approcher toujours mieux.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !