Comment les mathématiques permettent-elles de modéliser un phénomène périodique ?

Introduction

Les phénomènes périodiques sont partout autour de nous : le jour et la nuit, les saisons, les vibrations d’une corde. Pour les décrire et les comprendre, les mathématiques offrent de nombreux outils.

I. Comprendre la périodicité en mathématiques

1. Définition de la périodicité et exemples développés

On dit qu’une fonction [math]f[/math] est périodique s’il existe un réel [math]T > 0[/math] tel que :

f(x+T) = f(x) \quad \text{pour tout } x.

Le nombre [math]T[/math] est appelé une période de la fonction.

Exemples :

• [math]f(x) = \sin(x)[/math] vérifie [math]\sin(x+2\pi) = \sin(x)[/math], donc [math]2\pi[/math] est une période.
• [math]f(x) = \tan(x)[/math] est périodique de période [math]\pi[/math].
• Un pendule simple effectue un mouvement qui se répète toutes les [math]T = 2\pi \sqrt{\tfrac{L}{g}}[/math] secondes (avec [math]L[/math] la longueur, [math]g[/math] la gravité). On a donc une périodicité temporelle.

La périodicité traduit l’idée d’un phénomène qui revient à l’identique après un certain intervalle. C’est la base pour modéliser des mouvements cycliques, des saisons, des signaux électriques ou encore des ondes sonores.

2. Propriétés générales des fonctions périodiques

Au-delà des sinus et cosinus, toutes les fonctions périodiques partagent certaines propriétés mathématiques intéressantes.

• Symétrie et invariance
  Si [math]f[/math] est périodique de période [math]T[/math], alors elle a aussi pour période [math]kT[/math] pour tout entier [math]k \geq 1[/math].
  Exemple : [math]\sin(x)[/math] est de période [math]2\pi[/math], mais aussi [math]4\pi[/math], [math]6\pi[/math], etc.
• Moyenne sur une période
  On peut définir la valeur moyenne d’une fonction périodique sur une période :

\overline{f} = \tfrac{1}{T} \int_0^T f(x)dx.

Exemple :

\overline{\sin(x)} = \tfrac{1}{2\pi}\int_0^{2\pi}\sin(x)dx = 0.

Cette idée est utilisée en physique pour décrire des grandeurs «moyennes» comme la tension efficace en électricité.

II. Décomposer et analyser les phénomènes périodiques

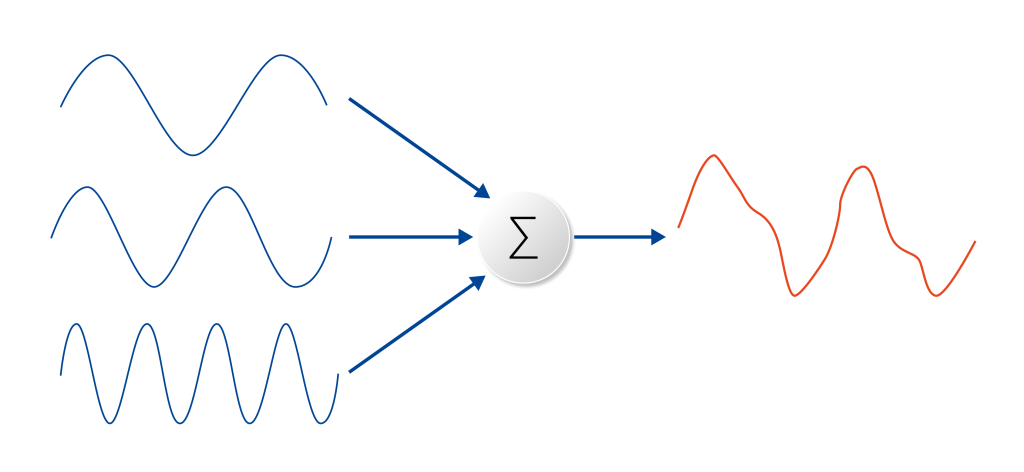
1. Superposition de signaux (principe de Fourier)

Jusqu’ici, nous avons vu que les fonctions sinus et cosinus permettent de modéliser des phénomènes simples comme un pendule ou une oscillation. Mais dans la réalité, de nombreux phénomènes périodiques sont beaucoup plus complexes : bruit, signaux électriques, ondes sonores…

Le mathématicien Joseph Fourier (1768–1830) a montré qu’on pouvait représenter tout signal périodique comme une combinaison de sinus et de cosinus de fréquences multiples.

Formellement, si [math]f(t)[/math] est une fonction périodique de période [math]T[/math], alors elle peut s’écrire sous la forme :

f(t) = a_0 + \sum_{n=1}^{\infty} \big( a_n \cos(n\omega t) + b_n \sin(n\omega t) \big),

où :

• [math]\omega = \tfrac{2\pi}{T}[/math] est la pulsation fondamentale,
• [math]a_n, b_n[/math] sont des coefficients appelés coefficients de Fourier, qui dépendent de la fonction étudiée.

Exemple concret : l’onde carrée

Une onde carrée est un signal qui alterne entre +1 et –1 à intervalles réguliers. Ce signal n’est pas une sinusoïde, et pourtant Fourier montre qu’il peut s’écrire comme une somme infinie de sinusoïdes :

f(t) = \tfrac{4}{\pi} \left( \sin(\omega t) + \tfrac{1}{3}\sin(3\omega t) + \tfrac{1}{5}\sin(5\omega t) + \cdots \right).

• Si on ne garde que [math]\sin(\omega t)[/math], on obtient une simple sinusoïde.
• En ajoutant [math]\sin(3\omega t)[/math] et [math]\sin(5\omega t)[/math], la fonction commence déjà à ressembler à une onde carrée.
• Plus on ajoute de termes, plus l’approximation devient précise.