Approximation de Pi

Introduction

On a tous déjà entendu parler de [math]\pi[/math], ce nombre mystérieux qui relie le cercle à son diamètre. Mais comme il a une infinité de décimales, les mathématiciens ont dû inventer plein de façons de l’approcher…

I. π : définitions et premières approximations

1. Définition géométrique et historique

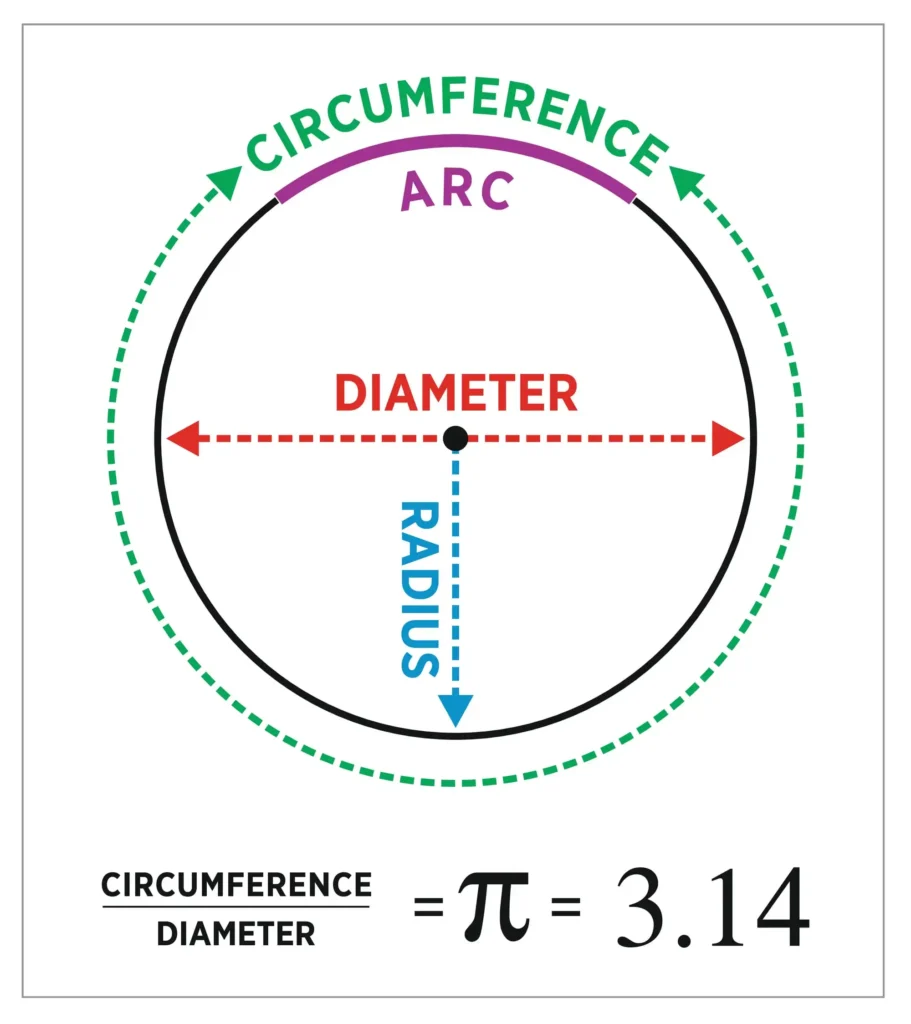
Le nombre [math]\pi[/math] est défini comme le rapport entre la circonférence d’un cercle et son diamètre :

\pi = \dfrac{\text{périmètre du cercle}}{\text{diamètre}}.

Ce rapport est le même pour tous les cercles, petits ou grands, et c’est ce qui en fait une constante universelle.

Depuis l’Antiquité, les civilisations ont essayé d’approcher [math]\pi[/math] :

• En Égypte, le papyrus Rhind (~-1650) donne [math]\pi \approx 3,16[/math].
• Archimède (-287 à -212) propose une méthode géométrique ingénieuse : il encadre le cercle par des polygones réguliers inscrits et circonscrits, puis calcule leur périmètre. En augmentant le nombre de côtés, on se rapproche de la circonférence du cercle. Résultat : il obtient [math]3,1408 < \pi < 3,1429[/math], une précision remarquable pour l’époque.

Mathématiquement, cette méthode consiste à créer une suite d’approximation : à mesure que le nombre de côtés augmente, la valeur trouvée converge vers [math]\pi[/math].

2. Propriétés et nature de [math]\pi[/math]

Au fil des siècles, les mathématiciens ont découvert des propriétés fondamentales de [math]\pi[/math] :

• En 1761, Lambert démontre que [math]\pi[/math] est irrationnel : il ne peut pas s’écrire comme une fraction [math]\tfrac{p}{q}[/math] d’entiers.
• En 1882, Lindemann prouve que [math]\pi[/math] est même transcendant : il n’est solution d’aucune équation polynomiale à coefficients entiers.

Ainsi, il est impossible de déterminer [math]\pi[/math] avec une fraction ou même une équation polynomiale.

La seule manière de l’approcher est donc d’utiliser :

• des séries infinies (comme la série de Leibniz ou de Machin),
• des fractions continues qui donnent de très bonnes approximations,
• ou des méthodes géométriques/probabilistes.

II. Méthodes mathématiques pour approximer [math]\pi[/math]

1. Approches géométriques et analytiques

À partir du XVIIe siècle, les mathématiciens trouvent des formules analytiques permettant de calculer [math]\pi[/math] directement à partir de séries infinies.

Exemple célèbre : la série de Leibniz :

\pi = 4\sum_{k=0}^{\infty} \frac{(-1)^k}{2k+1} = 4\left(1 - \tfrac{1}{3} + \tfrac{1}{5} - \tfrac{1}{7} + \dots \right).

Cette série est exacte mais converge très lentement : pour obtenir seulement 2 décimales correctes, il faut déjà plusieurs centaines de termes.

Pour gagner en efficacité, on utilise des identités trigonométriques comme celle de Machin (1706) :

\pi = 16\arctan\tfrac{1}{5} - 4\arctan\tfrac{1}{239}.