Le Dobble

Introduction

Vous connaissez sûrement le jeu Dobble : on retourne deux cartes et, à chaque fois, il y a toujours un symbole en commun. On pourrait croire que c’est juste un hasard bien conçu, mais en réalité, il y a des mathématiques très précises derrière. C’est ce que je vais vous montrer 🙂

I. Mini-Dobble à 7 cartes : incidence et vérifications concrètes (ordre 2)

L’idée est de commencer par un exemple réduit de Dobble : 7 cartes avec 7 symboles seulement. Cela permet de visualiser et de prouver les propriétés sans se perdre dans la complexité du vrai jeu.

1. Mise en place : la matrice d’incidence

On considère 7 cartes et 7 symboles, que l’on note [math]A, B, \dots, G[/math].

Pour représenter la répartition des symboles sur les cartes, on utilise une matrice d’incidence [math]M\in{0,1}^{7\times 7}[/math] :

• chaque ligne correspond à un symbole,
• chaque colonne correspond à une carte,
• [math]M_{i,j}=1[/math] si le symbole [math]i[/math] est présent sur la carte [math]j[/math], et [math]0[/math] sinon.

Dans ce mini-Dobble, chaque carte contient exactement 3 symboles, et chaque symbole apparaît exactement sur 3 cartes.

On a donc les propriétés :

\sum_i M_{i,j}=3 \quad \text{(3 symboles par carte)},

\sum_j M_{i,j}=3 \quad \text{(3 cartes par symbole)}

La règle du Dobble s’écrit joliment avec le produit scalaire :
si l’on prend deux colonnes [math]c\neq c'[/math], leur produit scalaire vaut toujours 1 :

\langle M_{\bullet c},M_{\bullet c'}\rangle = 1.

Autrement dit, deux cartes distinctes ont exactement un symbole en commun.

2. Lecture géométrique : le plan projectif d’ordre 2 (plan de Fano)

Ce mini-Dobble correspond exactement au plan de Fano, qui est le plus petit exemple de plan projectif (d’ordre 2).

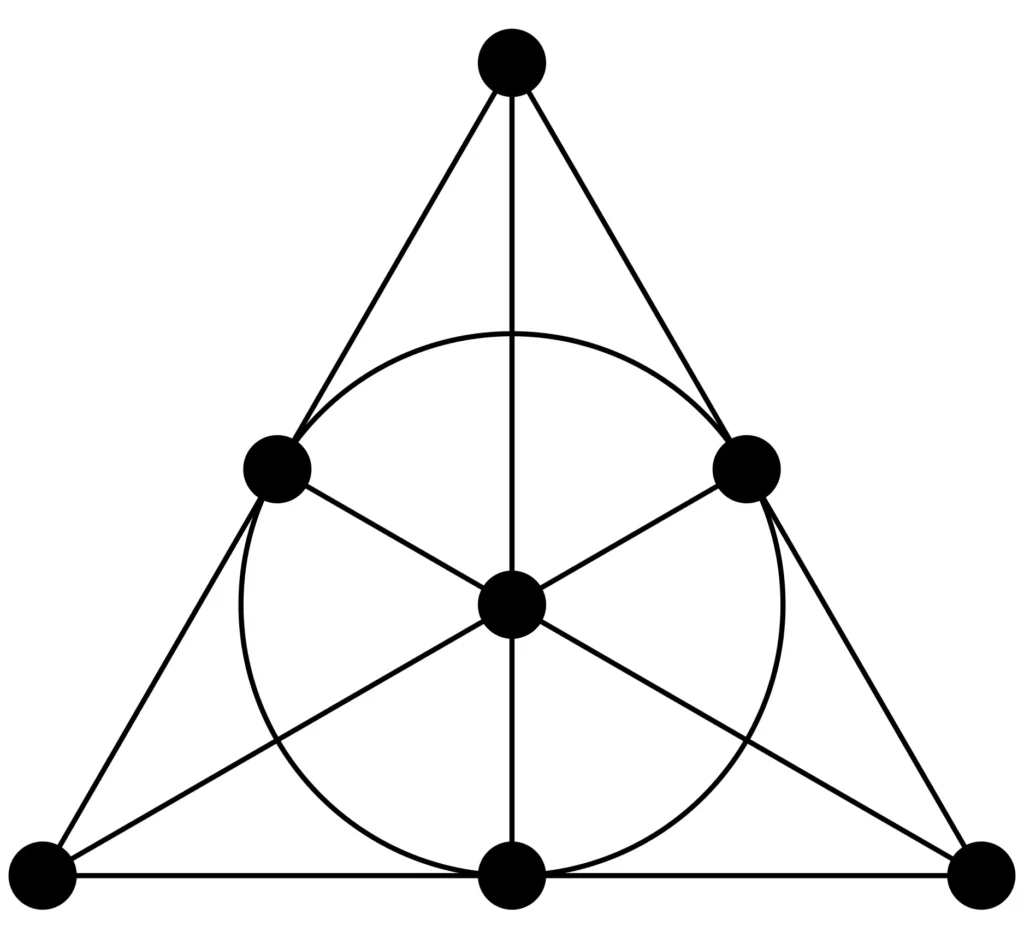
Un plan projectif repose sur trois axiomes fondamentaux :

1. Toute paire de lignes se coupe en un point unique.
2. Par toute paire de points passe exactement une ligne.
3. Il existe 4 points tels que pas plus de deux d’entre eux ne soient alignés (condition de non-dégénérescence).

On peut faire la correspondance suivante :

• Point = symbole ;
• Ligne = carte.

On obtient alors la structure suivante :

• 7 points, 7 lignes,
• 3 points sur chaque ligne,
• 3 lignes passant par chaque point.

Cela correspond exactement aux propriétés du mini-Dobble.

Une conséquence intéressante : si l’on choisit 3 points (donc 3 symboles) qui n’appartiennent pas à une même ligne, alors il n’existe aucune carte qui les regroupe.

Au passage, n’hésitez pas à aller regarder la vidéo ci-dessous qui illustre bien ce sujet sous forme vidéo :

II. Théorie générale : du mini-Dobble aux plans projectifs d’ordre [math]n[/math]

L’exemple du mini-Dobble à 7 cartes correspond au plan projectif d’ordre 2. On peut maintenant généraliser cette idée à un plan projectif d’ordre [math]n[/math].

1. Axiomes et paramètres

Un plan projectif d’ordre [math]n[/math] est une structure combinatoire qui respecte les axiomes :

1. Toute paire de lignes se coupe en un point unique.
2. Par toute paire de points passe une unique ligne.
3. La structure n’est pas dégénérée (il existe au moins 4 points dont pas plus de deux ne sont alignés).

De ces axiomes découlent les paramètres suivants :

• Nombre total de points (et de lignes) :
  [math]v = n^2+n+1[/math].
• Nombre de points par ligne (et de lignes par point) :
  [math]k = r = n+1[/math].
• Toute paire de points est sur une unique ligne :
  [math]\lambda = 1[/math].

2. Vue matricielle

On peut traduire tout cela dans une matrice d’incidence [math]M \in {0,1}^{v \times v}[/math], où les lignes représentent les points et les colonnes représentent les lignes (ou cartes, dans le langage Dobble).