Comment les mathématiques peuvent aider pour le traitement des cancers ?

Introduction

Le cancer fait peur parce qu’il touche énormément de personnes, mais on oublie souvent que derrière la médecine, il y a aussi… des mathématiques. Elles permettent de comprendre comment une tumeur grandit, de mesurer l’efficacité d’un traitement et même d’optimiser les doses de médicaments. L’idée est donc de voir comment les maths peuvent aider, concrètement, à mieux traiter les cancers.

I. Modéliser la croissance des cellules cancéreuses

1. Croissance exponentielle et logistique

La première idée, en mathématiques, est de modéliser la croissance d’une population de cellules comme une croissance exponentielle.

Si [math]N(t)[/math] désigne le nombre de cellules au temps [math]t[/math], alors on peut écrire :

N(t) = N_0 e^{rt}

où :

• [math]N_0[/math] est le nombre initial de cellules,
• [math]r[/math] est le taux de croissance (plus il est grand, plus la tumeur grossit vite).

Ce modèle correspond à une suite géométrique si l’on considère des pas de temps discrets (jour après jour).

Cependant, dans un organisme réel, cette croissance n’est pas illimitée : la tumeur finit par manquer d’espace, de nutriments ou être freinée par le système immunitaire. On utilise alors le modèle logistique :

N(t) = \dfrac{K}{1 + A e^{-rt}}

où :

• [math]K[/math] représente la capacité maximale (taille limite que la tumeur peut atteindre),
• [math]A[/math] dépend du nombre initial de cellules.

Contrairement à l’exponentielle, la courbe logistique commence par croître rapidement, puis se stabilise.

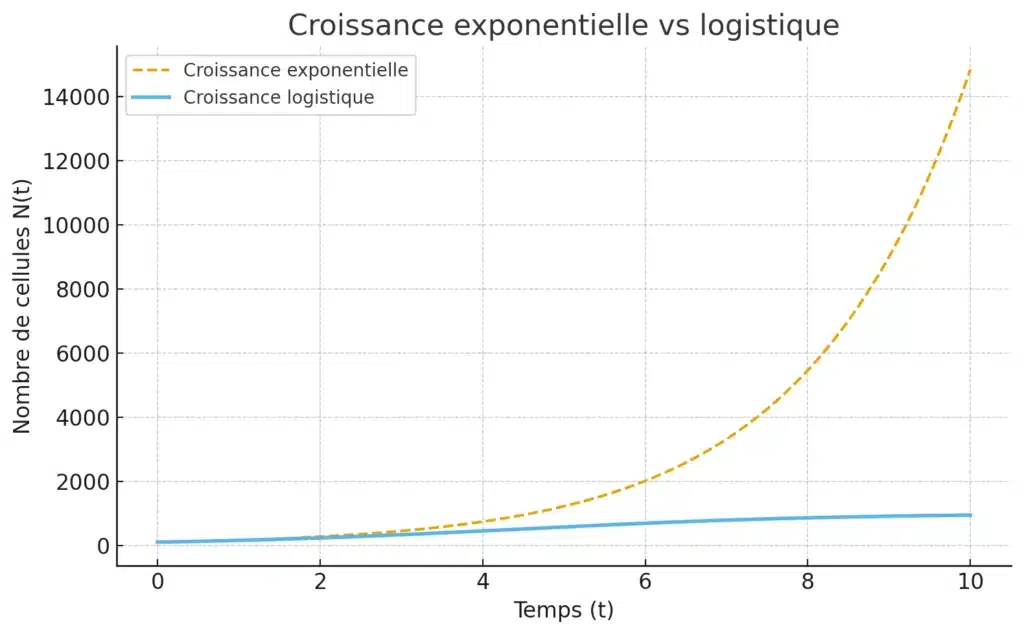
2. Intérêt médical de ces modèles

Ces modèles ont une véritable utilité médicale :

• Si le paramètre [math]r[/math] est grand, la tumeur est dite «agressive» → elle grossit très vite, et le traitement doit être mis en place rapidement.
• Si [math]r[/math] est petit, la croissance est plus lente → les médecins peuvent parfois observer l’évolution avant d’agir.

De plus, la forme logistique permet de mieux anticiper la taille future d’une tumeur et donc de décider du moment optimal pour intervenir.

II. Probabilités et statistiques : comprendre les traitements

1. Probabilité de survie et loi exponentielle

En médecine, on s’intéresse souvent à la durée de survie après un traitement.

On peut modéliser cette durée par une variable aléatoire [math]T[/math].

Un modèle simple est la loi exponentielle :

\mathbb{P}(T > t) = e^{-\lambda t}

Cela signifie que la probabilité qu’un patient survive plus de [math]t[/math] années diminue de façon exponentielle.

On peut calculer l’espérance de vie d’un patient dans ce modèle :

\mathbb{E}[T] = \dfrac{1}{\lambda}

Interprétation :

• si [math]\lambda[/math] est grand, la survie moyenne est courte → le traitement est peu efficace.
• si [math]\lambda[/math] est petit, la survie moyenne est longue → le traitement est plus efficace.

Ainsi, une simple formule mathématique permet de comparer l’impact de deux traitements différents sur l’espérance de vie.

Exemple numérique :

Supposons deux traitements différents :

• Traitement A : [math]\lambda = 0{,}2[/math]
  [math]\mathbb{E}[T] = \dfrac{1}{0{,}2} = 5[/math] ans en moyenne.
• Traitement B : [math]\lambda = 0{,}1[/math]
  [math]\mathbb{E}[T] = \dfrac{1}{0{,}1} = 10[/math] ans en moyenne.

Cela signifie que le traitement B double l’espérance de vie par rapport au traitement A (en moyenne évidemment, rien n’est sûr).