Hôtel de Hilbert : l’infini en maths

Introduction

🛎️ Imaginez un hôtel avec une infinité de chambres… toutes occupées ! Que se passe-t-il si un nouveau client arrive ? Et si une infinité de clients, ou même une infinité de bus, veulent aussi une chambre ?

C’est le paradoxe de l’Hôtel de Hilbert, une expérience de pensée qui révèle à quel point l’infini peut réserver des surprises en mathématiques.

I. La première surprise de l’infini

1. Rappel de la définition d’une bijection

En mathématiques, une bijection est une fonction qui met en correspondance chaque élément d’un ensemble avec un et un seul élément d’un autre ensemble, et réciproquement.

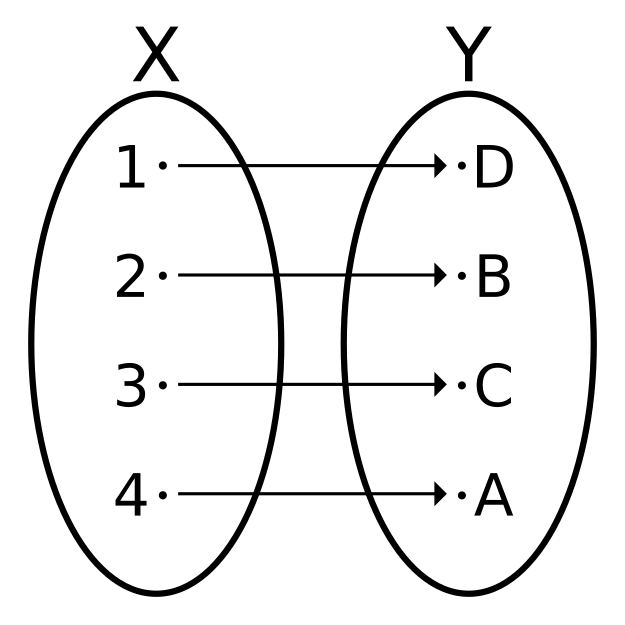
Autrement dit, personne n’est oublié, et personne n’a deux places : chaque élément d’un côté a exactement un partenaire de l’autre côté.

Un exemple simple est la fonction :

f(n) = n - 1.

• Ici, [math]f[/math] est définie de [math]\mathbb{N}^*[/math] (les entiers naturels non nuls, avec 1, 2, …) vers [math]\mathbb{N}[/math] (les entiers naturels, donc 0, 1, 2, 3, …).
• Si on commence à [math]n=1[/math], alors [math]f(1)=0[/math], [math]f(2)=1[/math], [math]f(3)=2[/math], etc.

En fait, on peut aussi considérer la fonction inverse :

g(n) = n + 1,

qui est une bijection de [math]\mathbb{N}[/math] vers [math]\mathbb{N}^*[/math].

2. Lien avec l’hôtel

Imaginons maintenant l’hôtel de Hilbert, un hôtel avec une infinité de chambres, toutes occupées.

Un nouveau client arrive : comment lui trouver une chambre ?

• On demande à chaque client de la chambre [math]n[/math] d’aller dans la chambre [math]n+1[/math].
• Ainsi, le client de la chambre 1 va dans la chambre 2, celui de la chambre 2 va dans la chambre 3, etc.
• Toutes les chambres restent occupées… sauf la chambre 1, qui se libère pour accueillir le nouveau client.

Ce simple décalage illustre bien l’idée qu’avec la bijection précédente, on peut toujours «faire de la place».

II. Quand une infinité de nouveaux clients arrive…

1. Stratégie 1 : multiplier par 2

Imaginons maintenant que toute une infinité de nouveaux clients se présente à l’hôtel, alors que toutes les chambres sont déjà occupées.

Une solution astucieuse est de demander à chaque client actuel de la chambre [math]n[/math] d’aller dans la chambre [math]2n[/math].

• Ainsi, le client de la chambre 1 va dans la chambre 2, celui de la chambre 2 va dans la chambre 4, celui de la chambre 3 va dans la chambre 6, etc.
• Toutes les chambres paires sont maintenant occupées.
• Par contre, toutes les chambres impaires (1, 3, 5, …) se sont libérées !

On peut donc loger l’infinité de nouveaux clients en leur donnant les chambres impaires, selon la règle :

i \mapsto 2i - 1

2. Stratégie 2 : une infinité de bus d’infinité de clients