Comment déterminer l’heure de décès d’une personne ?

Introduction

La criminologie fascine souvent parce qu’elle mêle enquête, sciences et un peu de mystère. Parmi les questions clés auxquelles doivent répondre les experts : à quelle heure une personne est-elle morte ? Cette estimation est essentielle pour une enquête judiciaire, et étonnamment… les mathématiques jouent un rôle majeur.

En effet, après la mort, le corps humain se refroidit progressivement jusqu’à atteindre la température ambiante. Ce phénomène peut être modélisé par des outils que l’on étudie au lycée : fonctions exponentielles, suites, statistiques.

Problématique : comment les mathématiques, en particulier les fonctions exponentielles et les statistiques, permettent-elles de modéliser le refroidissement d’un corps et d’estimer l’heure de décès ?

I. La température du corps : une décroissance modélisable

1. Refroidissement du corps = décroissance exponentielle

Après la mort, le corps humain cesse de produire de la chaleur et sa température diminue progressivement pour tendre vers celle de son environnement.

Mathématiquement, ce type de phénomène est bien représenté par une décroissance exponentielle :

T(t) = T_{\text{ext}} + (T_0 - T_{\text{ext}})\times e^{-kt}.

• [math]T(t)[/math] : température du corps au temps [math]t[/math] (en heures après la mort),
• [math]T_{\text{ext}}[/math] : température ambiante,
• [math]T_0[/math] : température initiale du corps (≈ 37°C),
• [math]k[/math] : constante de refroidissement (dépend de la corpulence, vêtements, environnement).

2. Exemple concret d’application

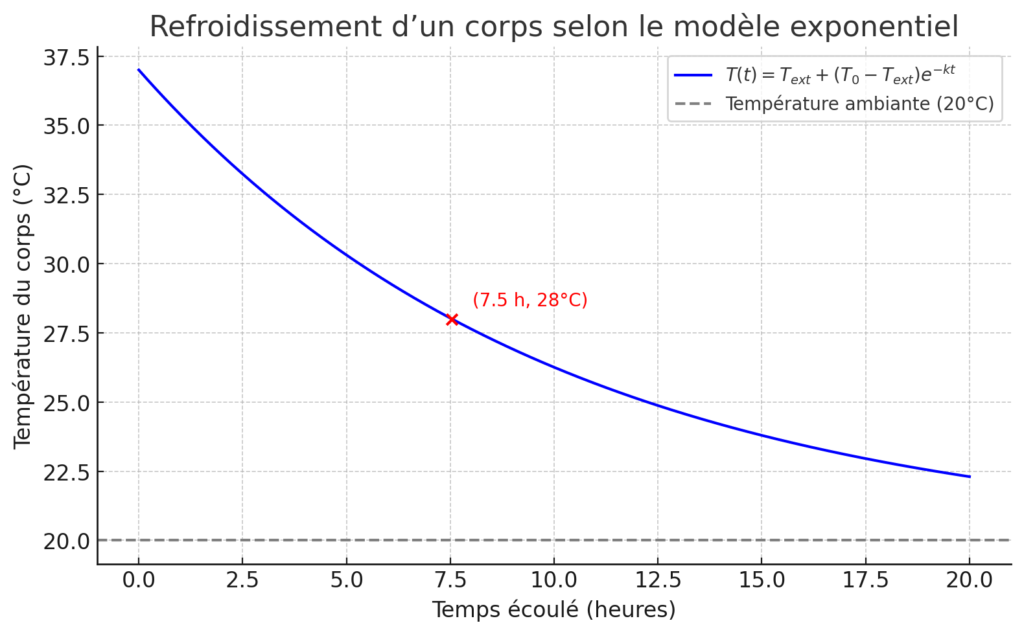
Imaginons un corps retrouvé dans une pièce à [math]20^\circ C[/math], avec une température mesurée du corps de [math]28^\circ C[/math].

On suppose [math]T_0 = 37^\circ C[/math] et une constante de refroidissement [math]k = 0,1 h^{-1}[/math].

Formule :

T(t) = 20 + (37 - 20)\times e^{-0,1t}.

Donc :

T(t) = 20 + 17 e^{-0,1t}.

On veut trouver [math]t[/math] tel que [math]T(t) = 28[/math].

28 = 20 + 17 e^{-0,1t}

8 = 17 e^{-0,1t}

e^{-0,1t} = \tfrac{8}{17}

-0,1t = \ln\left(\tfrac{8}{17}\right)

t = -\tfrac{1}{0,1}\ln\left(\tfrac{8}{17}\right)

Calcul numérique :

t \approx -10 \times \ln(0,47) \approx 7,5 \text{ heures}.

Cela signifie que la personne est probablement morte environ 7 heures et 30 minutes avant la découverte du corps. Par exemple, si le corps a été trouvé à 7h du matin, le décès aurait eu lieu vers 23h30 la veille.

II. Les statistiques pour réduire l’incertitude

1. Variabilité des mesures

La méthode du refroidissement n’est jamais exacte à la minute près.

En effet, la température d’un corps dépend de plusieurs facteurs :

• les vêtements (un manteau ralentit le refroidissement),
• la corpulence (plus une personne est massive, plus le refroidissement est lent),
• l’environnement (un corps dans une pièce à 25 °C ne se refroidit pas comme à 10 °C).

Résultat : deux personnes mortes à la même heure peuvent présenter des températures légèrement différentes.