Dans quelle mesure le résultat d’un sondage peut-il être fiable ?

Introduction
Les sondages occupent une place essentielle dans nos sociétés : intentions de vote, habitudes de consommation, enquêtes d’opinion… Mais peut-on vraiment leur faire confiance ? 🤔
En fait, derrière chaque sondage, il y a des mathématiques : elles permettent de transformer un échantillon de personnes en une estimation pour toute une population. Cela soulève immédiatement deux questions : en quoi les mathématiques nous servent-elles pour faire des sondages ? et en quoi les mathématiques nous aident-elles à en analyser la fiabilité ?
Problématique : dans quelle mesure le résultat d’un sondage peut-il être fiable ?
I. Un sondage, c’est une somme de variables aléatoires
1. Modéliser un sondage
Un sondage, c’est simplement poser une question à plusieurs personnes, puis compter leurs réponses.
Pour le modéliser en maths, on utilise des variables aléatoires :
- On note [math]X_i = 1[/math] si la personne sondée répond « oui ».
- On note [math]X_i = 0[/math] si elle répond « non ».
Si chaque personne est choisie de manière indépendante et a la même probabilité [math]p[/math] de répondre « oui », alors la somme des réponses [math]X = X_1 + X_2 + \cdots + X_n[/math] suit une loi binomiale : [math]X \sim \mathcal{B}(n,p)[/math].
Autrement dit, [math]X[/math] représente le nombre total de « oui » obtenus sur [math]n[/math] personnes.
Les formules classiques donnent alors :
- Espérance : [math]\mathbb{E}(X) = np[/math].
- Variance : [math]\mathrm{Var}(X) = np(1-p)[/math].
2. La proportion observée
Dans un sondage, ce qui nous intéresse n’est pas seulement le nombre de « oui », mais la proportion de « oui » : [math]\hat{p} = \frac{X}{n}[/math].
On peut montrer que :
- Espérance : [math]\mathbb{E}(\hat{p}) = p[/math] → donc en moyenne, notre sondage reflète bien la vraie proportion de la population.
- Variance : [math]\mathrm{Var}(\hat{p}) = \frac{p(1-p)}{n}[/math].
Cela veut dire que plus [math]n[/math] est grand, plus la variance diminue, et donc plus le sondage est fiable.
Exemple numérique
Prenons un sondage avec [math]n = 1000[/math] personnes et supposons que la vraie proportion est [math]p = 0,5[/math].
On calcule l’écart-type :
\sigma_{\hat{p}} = \sqrt{\frac{p(1-p)}{n}} = \sqrt{\frac{0,5 \times 0,5}{1000}} \approx 0,016.Cela veut dire que la proportion mesurée dans un sondage peut naturellement varier de ±1,6% autour de la vraie valeur, uniquement à cause du hasard d’échantillonnage.
II. La notion de marge d’erreur
1. Intervalle de confiance à 95 %
Quand on réalise un sondage, on calcule une proportion observée [math]\hat{p}[/math]. Mais cette valeur n’est qu’une estimation : elle varie selon les personnes interrogées, à cause du hasard d’échantillonnage.
Mathématiquement, on peut montrer que si l’échantillon est assez grand, la variable [math]\hat{p}[/math] suit une loi qui ressemble beaucoup à une loi normale centrée sur [math]p[/math], avec un écart-type :
\sigma_{\hat{p}} = \sqrt{\tfrac{\hat{p}(1-\hat{p})}{n}}.Cela permet de construire ce qu’on appelle un intervalle de confiance.
À 95 %, la formule est :
\hat{p} \pm 1,96 \cdot \sqrt{\tfrac{\hat{p}(1-\hat{p})}{n}}.Exemple :
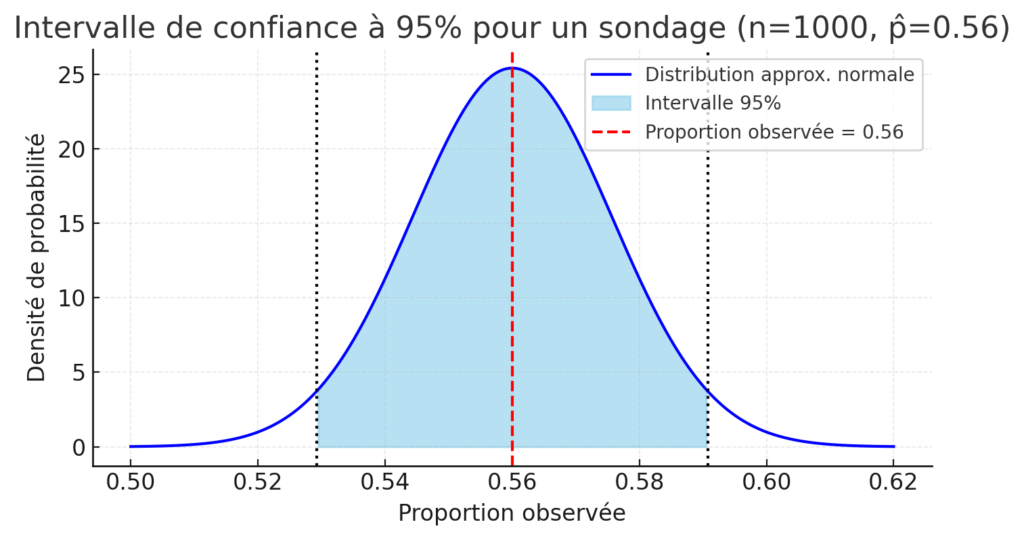
Un sondage auprès de [math]n=1000[/math] personnes donne [math]\hat{p}=0,56[/math] (56 %).
On calcule :
\sqrt{\tfrac{0,56 \times 0,44}{1000}} \approx 0,016.La marge d’erreur est donc : [math]1,96 \times 0,016 \approx 0,03[/math] (soit 3 %).
On obtient l’intervalle : [math][0,53 ; 0,59][/math].
2. Impact de la taille de l’échantillon
La précision du sondage dépend fortement de la taille [math]n[/math].
En effet, l’écart-type de la proportion est :
\sigma_{\hat{p}} = \sqrt{\tfrac{p(1-p)}{n}} \propto \tfrac{1}{\sqrt{n}}.Ainsi, plus [math]n[/math] est grand, plus la marge d’erreur est petite.
Comparaison (pour une proportion proche de 50 %) :
- [math]n = 100[/math] → marge d’erreur ≈ ±10 %.
- [math]n = 1000[/math] → marge d’erreur ≈ ±3 %.
- [math]n = 10 000[/math] → marge d’erreur ≈ ±1 %.
On voit donc que multiplier par 10 la taille de l’échantillon divise seulement par 3 l’erreur, à cause de la racine carrée.
III. Les limites et biais des sondages
1. Le biais d’échantillonnage
Jusqu’ici, on a supposé que les personnes interrogées étaient choisies au hasard, de manière parfaitement représentative de la population. Mais dans la réalité, ce n’est pas toujours le cas.
Exemple : si un sondage politique interroge surtout des jeunes urbains, il risque de surestimer certains partis et de sous-estimer d’autres.
Mathématiquement, même si [math]n \to \infty[/math] (autrement dit, même si on prend un échantillon gigantesque), la proportion mesurée [math]\hat{p}[/math] restera fausse si la base de sondage n’est pas représentative. On parle alors de biais d’échantillonnage : il ne disparaît pas avec la taille de l’échantillon.
2. Proportions rares et incertitude relative
Un autre problème apparaît quand on s’intéresse à de petites proportions.
Exemple : supposons qu’un parti recueille environ 2 % des intentions de vote dans la population. On interroge [math]n=1000[/math] personnes.
La marge d’erreur est alors d’environ ±1 %.
Résultat : l’intervalle de confiance est [1 % ; 3 %].
En valeur absolue, c’est seulement ±1 %. Mais en valeur relative, l’incertitude est énorme : entre 50 % de moins (1 % au lieu de 2) et 50 % de plus (3 % au lieu de 2) !
C’est pour cela que les sondages sur les « petits partis » ou proches d’un seuil d’éligibilité sont particulièrement délicats à interpréter : l’incertitude relative est beaucoup plus grande que pour des partis majoritaires.
Conclusion
- Les sondages reposent sur des outils mathématiques solides : probabilités, espérance, variances, intervalles de confiance.
- Leur fiabilité dépend directement de la taille de l’échantillon… mais surtout de sa représentativité.
- Les mathématiques permettent donc de mesurer l’incertitude, mais elles ne garantissent pas la vérité absolue d’un sondage.
On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !








