Comment les mathématiques aident-elles à détecter la fraude fiscale ? (Loi de Benford)

Introduction

Lutter contre la fraude fiscale, c’est un vrai défi : chaque année, des milliards d’euros échappent aux États à cause de comptes truqués, de fausses factures ou de chiffres arrangés. Mais les fraudeurs oublient souvent une chose… les mathématiques, elles, ne mentent jamais.

En effet, lorsqu’on observe des données réelles, les chiffres suivent des régularités surprenantes. C’est ce qu’on appelle la loi de Benford

Problématique : dans quelle mesure la loi de Benford et d’autres méthodes statistiques permettent-elles de repérer une fraude fiscale ?

I. Les nombres et leurs régularités cachées

1. Une intuition surprenante

Exemple rapide : sur les factures d’électricité, on trouve bien plus de montants commençant par 1 (120€, 180€…) que par 9 (930€, 980€…). Étonnant non ?

Instinctivement, on aurait tendance à croire que chaque chiffre de 1 à 9 a la même chance d’apparaître en premier (environ 11,1% chacun). On appelle ça le biais d’équiprobabilité.

Mais en réalité… ce n’est pas du tout le cas !

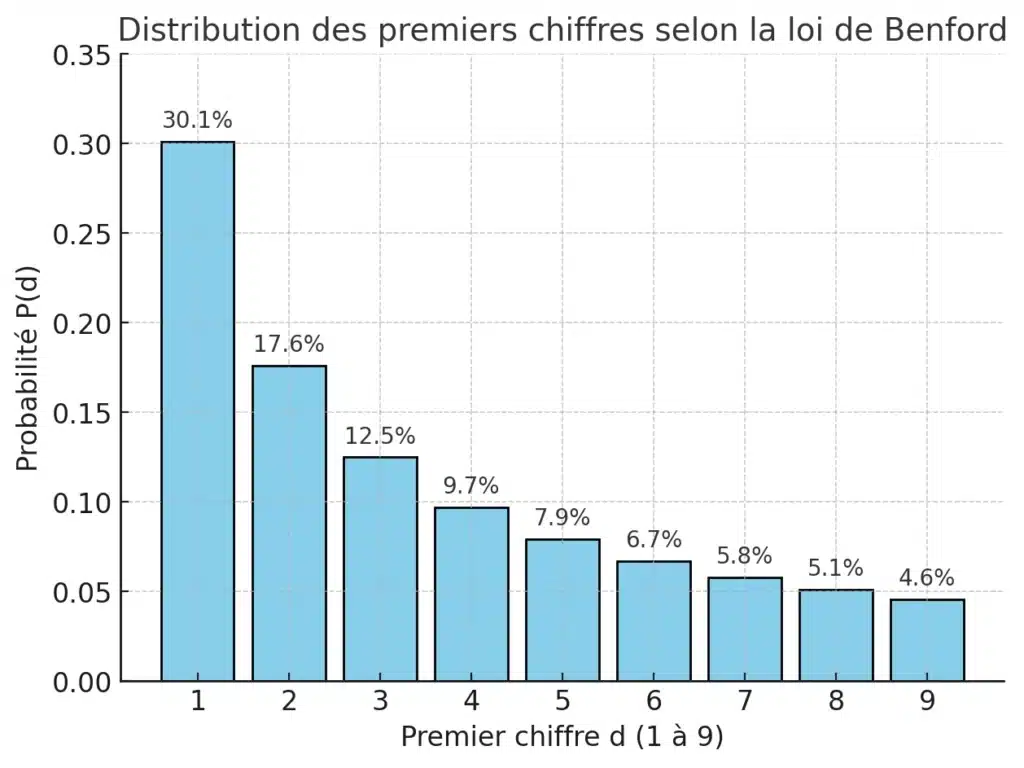
Comment comprendre cette non-uniformité ?

• Entre 1 et 2, on double la valeur → +100% d’augmentation.
• Entre 9 et 10, on ajoute seulement +11,1%.

Résultat : l’intervalle [1 ; 2] « couvre » plus de nombres significatifs que l’intervalle [9 ; 10].

2. La loi de Benford

La loi de Benford décrit la répartition des premiers chiffres dans de nombreux ensembles de données (ce n’est pas non plus applicable partout, on le verra dans la suite).

En fait, cette loi a été observée dès 1881 par l’astronome américain Simon Newcomb, qui avait remarqué que les premières pages (donc celles qui commençaient par 1, 2…) des tables de logarithmes étaient plus usées que les autres. Mais son article est passé inaperçu.

Ce n’est qu’en 1938 que Frank Benford a redécouvert le phénomène, en analysant des milliers de données réelles (longueurs de fleuves, cours de Bourse, etc.). C’est son nom qui est resté, même si l’idée vient de Newcomb.

Si l’on note [math] d [/math] le premier chiffre d’un nombre, la loi affirme que la probabilité qu’un nombre commence par [math] d [/math] est donnée par la formule :

P(d) = \log_{10}\Big(1 + \tfrac{1}{d}\Big)

où [math] d \in {1,2,\dots,9} [/math].

Concrètement :

• [math] P(1) = \log_{10}(2) \approx 0.301 [/math] → environ 30% des nombres commencent par 1.
• [math] P(9) = \log_{10}(10/9) \approx 0.046 [/math] → à peine 4,6% des nombres commencent par 9.

On retombe donc exactement sur ce que montrait l’histogramme précédent (de façon empirique) : une décroissance nette du chiffre 1 vers le chiffre 9.

Voici une vidéo super intéressante à consulter pour bien comprendre ! Elle peut aussi vous donner une idée concrète de la façon dont vous pourriez présenter pour rendre ça un peu plus vivant.

II. Détecter l’anormal dans les données fiscales

1. Les tests statistiques : comparer théorie et pratique

Imaginons une entreprise X qui déclare 1 000 montants de factures à l’administration fiscale. On extrait les premiers chiffres de ces montants et on les compare à la loi de Benford.

Principe du test du [math]\chi^2[/math] :

On calcule, pour chaque chiffre [math]d[/math], l’écart entre la fréquence observée [math]O_d[/math] et la fréquence théorique [math]E_d[/math] donnée par Benford.

La statistique est :

\chi^2 = \sum_{d=1}^9 \frac{(O_d - E_d)^2}{E_d}

• Si [math]\chi^2[/math] est petit → les données suivent bien Benford → pas de raison de suspecter une fraude.
• Si [math]\chi^2[/math] est grand → la répartition est trop différente → alerte possible.