La trompette de Gabriel
Introduction
On imagine souvent que ce qui est infini occupe une place infinie. Pourtant, la trompette de Gabriel est un objet mathématique surprenant : elle s’étend à l’infini, mais son volume reste fini… alors que sa surface est infinie ! Ce paradoxe, étudié dès le XVIIᵉ siècle, montre comment les mathématiques nous aident à comprendre l’infini au-delà des intuitions.
I. Présentation et paradoxe de la trompette de Gabriel
1. Définition de l’objet mathématique
On s’intéresse à la fonction [math]f(x) = \tfrac{1}{x}[/math], définie pour [math]x \geq 1[/math].
- Cette fonction est décroissante : plus [math]x[/math] est grand, plus [math]f(x)[/math] se rapproche de 0.
- Elle possède une asymptote horizontale : la droite d’équation [math]y=0[/math]. Cela signifie que la courbe se rapproche de l’axe des abscisses sans jamais le toucher.
Imaginons maintenant que l’on fasse tourner cette courbe autour de l’axe des abscisses, un peu comme si on faisait tourner une ficelle tendue autour d’un bâton. On obtient alors un solide de révolution qui s’étend indéfiniment vers la droite : c’est la trompette de Gabriel, aussi appelée trompette de Torricelli, du nom du mathématicien italien Evangelista Torricelli qui l’a inventée en 1640.
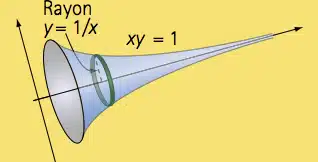
Cet objet a la forme d’un entonnoir interminable, ou d’une trompette sans fin.
- Son extrémité à gauche est bornée (au niveau de [math]x=1[/math]).
- Mais son «pavillon» s’étend à l’infini vers la droite, car la courbe [math]1/x[/math] ne s’arrête jamais.
L’idée intuitive est donc celle d’un solide infini en longueur, puisqu’il se prolonge sans limite, mais dont les dimensions transversales (la hauteur [math]1/x[/math]) deviennent de plus en plus petites.
2. La contradiction apparente
Là où cet objet devient fascinant, c’est lorsqu’on s’intéresse à deux caractéristiques géométriques :
- le volume de la trompette (l’espace intérieur qu’elle occupe),
- et l’aire de sa surface (la quantité de « matière » nécessaire pour recouvrir ses parois).
On pourrait naturellement penser que si la trompette est infinie en longueur, alors son volume doit lui aussi être infini. Or, ce n’est pas le cas : les mathématiques montrent que ce volume est fini (on démontrera plus tard qu’il vaut exactement [math]\pi[/math]).
En revanche, l’aire de la surface de cette trompette, elle, est infinie. Autrement dit :
- le solide pourrait théoriquement contenir une quantité limitée de peinture (volume fini),
- mais il faudrait une quantité infinie de peinture pour recouvrir sa paroi (surface infinie).
C’est ce paradoxe qui fait toute la réputation de la trompette de Gabriel : un objet qui tient dans un volume fini mais qui ne peut pas être recouvert.
Historiquement, ce paradoxe a été étudié au XVIIᵉ siècle par Evangelista Torricelli (1608–1647), disciple de Galilée. Il fut l’un des premiers à montrer, grâce aux méthodes naissantes du calcul infinitésimal, que l’infini ne se comporte pas toujours comme l’intuition le suggère. Son étude illustre bien la rupture entre la géométrie classique (figures finies) et l’analyse moderne (manipulation des infinis par les limites et les intégrales).
II. Étude mathématique : calculs d’aire et de volume
1. Calcul du volume fini
On reprend la fonction [math]f(x) = \tfrac{1}{x}[/math] définie pour [math]x \geq 1[/math]. Si on fait tourner cette courbe autour de l’axe des abscisses, on obtient un solide de révolution.
La formule du volume est :
V = \pi \int_1^{+\infty} (f(x))^2 dx.C’est une intégrale généralisée, donc pour travailler proprement on introduit une borne [math]n \geq 1[/math] :
V(n) = \pi \int_1^n \left(\tfrac{1}{x}\right)^2 dx = \pi \int_1^n \tfrac{1}{x^2} dx.Calcul de l’intégrale
On sait que :
\int \tfrac{1}{x^2} dx = -\tfrac{1}{x}.Donc :
V(n) = \pi \left[ -\tfrac{1}{x} \right]_1^n = \pi \left(-\tfrac{1}{n} - (-1)\right).V(n) = \pi \left(1 - \tfrac{1}{n}\right).Passage à la limite
Quand [math]n \to +\infty[/math] :
- le terme [math]\tfrac{1}{n}[/math] devient de plus en plus petit,
- donc [math]V(n)[/math] se rapproche de [math]\pi[/math].
En langage mathématique :
\lim_{n \to +\infty} V(n) = \lim_{n \to +\infty} \pi \left(1 - \tfrac{1}{n}\right) = \pi.2. Aire infinie de la surface
On cherche l’aire de la surface extérieure du solide. La formule est :
A = 2\pi \int_1^{+\infty} f(x)\sqrt{1 + (f'(x))^2} dx.Avec [math]f(x) = \tfrac{1}{x}[/math] et [math]f'(x) = -\tfrac{1}{x^2}[/math], on obtient :
A = 2\pi \int_1^{+\infty} \tfrac{1}{x} \sqrt{1 + \tfrac{1}{x^4}} dx.Idée de la démonstration : comparer à une intégrale connue
Pour tout [math]x \geq 1[/math], on a :
\sqrt{1 + \tfrac{1}{x^4}} \geq 1.Donc :
\tfrac{1}{x}\sqrt{1 + \tfrac{1}{x^4}} \geq \tfrac{1}{x}.En multipliant par [math]2\pi[/math], on obtient :
2\pi \cdot \tfrac{1}{x}\sqrt{1 + \tfrac{1}{x^4}} \geq 2\pi \cdot \tfrac{1}{x}.Conséquence sur l’intégrale
Pour tout entier [math]n \geq 1[/math] :
\int_1^n \tfrac{1}{x}\sqrt{1 + \tfrac{1}{x^4}} dx \geq \int_1^n \tfrac{1}{x} dx.Or, on sait que :
\int_1^n \tfrac{1}{x} dx = \ln(n).Donc :
\int_1^n \tfrac{1}{x}\sqrt{1 + \tfrac{1}{x^4}} dx \geq \ln(n).Passage à la limite
Quand [math]n \to +\infty[/math], on a :
\ln(n) \to +\infty.
Donc, par inégalité, l’intégrale
\int_1^{+\infty} \tfrac{1}{x}\sqrt{1 + \tfrac{1}{x^4}} dx.diverge aussi vers +∞.
Finalement :
A = 2\pi \int_1^{+\infty} \tfrac{1}{x}\sqrt{1 + \tfrac{1}{x^4}} dx = +\infty.III. Réflexions et prolongements
1. Interprétation et portée du paradoxe
La trompette de Gabriel montre un contraste frappant entre la géométrie intuitive et l’analyse mathématique.
- On pourrait croire que si un objet a une surface infinie, alors son volume doit aussi être infini.
- Or, ici c’est l’inverse : le volume [math]V = \pi[/math] est fini, tandis que l’aire [math]A = +\infty[/math].
Cela illustre l’importance des notions de convergence et divergence d’intégrales.
- Pour le volume, on intègre [math]\tfrac{1}{x^2}[/math], dont l’intégrale converge sur [math][1,+\infty[[/math].
- Pour la surface, on intègre un terme équivalent à [math]\tfrac{1}{x}[/math], dont l’intégrale diverge.
2. Applications et ouverture
Ce paradoxe n’est pas seulement une curiosité mathématique, il a aussi des résonances plus larges.
- En physique : on peut imaginer des objets qui auraient un volume fini mais une surface infinie. Théoriquement, il suffirait d’une quantité finie de peinture pour les remplir, mais une quantité infinie pour les recouvrir. Bien sûr, dans la réalité, les lois de la matière ne permettent pas un tel objet, mais l’exemple reste parlant pour montrer les limites de l’intuition.
- En mathématiques :
- Cela rappelle d’autres paradoxes liés à l’infini, comme l’hôtel de Hilbert, où un hôtel avec une infinité de chambres peut toujours accueillir de nouveaux clients.
- On peut aussi faire le lien avec certaines suites numériques : par exemple, la suite [math]u_n = \tfrac{1}{n^2}[/math] a une somme finie (la série converge), alors que la suite [math]v_n = \tfrac{1}{n}[/math] diverge, bien que ses termes tendent aussi vers 0.
- En ouverture :
L’étude de la trompette de Gabriel invite à réfléchir sur le rôle de l’infini en mathématiques et en physique. Comment comprendre et manipuler l’infini sans tomber dans les pièges de l’intuition naïve ?
Conclusion
La trompette de Gabriel nous montre que l’infini ne se comporte pas toujours comme on l’imagine. Grâce aux outils des intégrales et des limites, on comprend qu’un solide peut avoir un volume fini tout en ayant une surface infinie.
On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !








