Les femmes et les mathématiques

Introduction

Quand on parle de grands mathématiciens, on cite souvent des noms comme Euclide, Newton ou Gauss. Mais on oublie parfois que des femmes ont aussi marqué l’histoire des mathématiques, souvent dans l’ombre et malgré de nombreux obstacles.

I. Une histoire de persévérance

1. Les obstacles rencontrés

Pendant longtemps, les femmes ont été quasiment exclues du monde académique. Elles n’avaient pas le droit d’assister aux cours d’université, d’entrer dans les académies scientifiques, ni même de signer leurs travaux sous leur propre nom.

Un exemple marquant est celui de Sophie Germain (1776–1831). Passionnée de mathématiques, elle étudiait en cachette les cours de l’École polytechnique, alors interdite aux femmes. Pour correspondre avec le grand mathématicien Gauss, elle dut utiliser un pseudonyme masculin, «Monsieur LeBlanc», afin d’être prise au sérieux.

2. Quelques figures marquantes

Malgré ces obstacles, plusieurs femmes ont marqué l’histoire des mathématiques :

• Hypatie d’Alexandrie (IVe siècle) : philosophe et mathématicienne, elle a travaillé sur la géométrie et l’astronomie. Elle est considérée comme l’une des premières femmes scientifiques connues de l’histoire.
• Ada Lovelace (XIXe siècle) : elle a collaboré avec Charles Babbage sur sa «machine analytique», un ancêtre de l’ordinateur. Ses notes contiennent ce que l’on considère aujourd’hui comme le premier programme informatique.

Ces femmes ne se sont pas seulement battues pour avoir le droit d’exister dans le monde des sciences : elles ont aussi produit des résultats mathématiques majeurs. Et c’est justement ce que l’on peut illustrer à travers deux figures incontournables : Sophie Germain et Emmy Noether.

II. Deux femmes, deux découvertes

1. Sophie Germain et les nombres premiers

Sophie Germain (1776-1831) est une mathématicienne française qui a travaillé sur le dernier théorème de Fermat :

x^n + y^n = z^n \text{ n’a pas de solutions entières non triviales pour } n>2.

Son idée clé a été d’introduire ce qu’on appelle aujourd’hui les nombres premiers de Sophie Germain :
un nombre premier [math]p[/math] tel que [math]2p+1[/math] soit aussi premier.

Exemple :

• [math]11[/math] est un nombre premier,
• [math]2\times 11+1=23[/math] est aussi premier, donc [math]11[/math] est un nombre premier de Sophie Germain.

Grâce à cette notion, elle a pu montrer que pour une infinité de nombres premiers [math]p[/math], certaines solutions de l’équation de Fermat étaient impossibles (on appelle cela le «premier cas» du théorème). C’était une avancée majeure à l’époque, car personne n’avait réussi à progresser de façon générale sur ce problème vieux de plusieurs siècles.

Aujourd’hui encore, les nombres premiers de Sophie Germain sont utilisés, notamment en cryptographie moderne, car ils permettent de construire des clés robustes pour protéger les communications.

2. Emmy Noether et les symétries → lois de conservation

Le théorème de Noether dit qu’à chaque symétrie d’un système physique correspond une loi de conservation.

Prenons un exemple accessible : le mouvement d’une planète autour du Soleil.

• La gravitation newtonienne est invariante par rotation : si l’on fait tourner le système, rien ne change.
• Cela implique la conservation du moment angulaire.

Démonstration (loi des aires de Kepler)

Notons :

• [math]r[/math] : la distance Soleil–planète,
• [math]v_t[/math] : la vitesse tangentielle de la planète,
• [math]m[/math] : la masse de la planète.

Le moment angulaire se définit par :

L = m \cdot r \cdot v_t.

Or, la gravitation étant une force centrale (dirigée vers le Soleil), elle n’exerce aucun moment :

\dfrac{dL}{dt} = 0 \quad \Rightarrow \quad L = \text{constante}.

Ainsi, le produit [math]r \times v_t[/math] reste constant tout au long du mouvement.

• Quand [math]r[/math] est petit (proche du Soleil), [math]v_t[/math] doit être grand.
• Quand [math]r[/math] est grand, [math]v_t[/math] est plus petit.

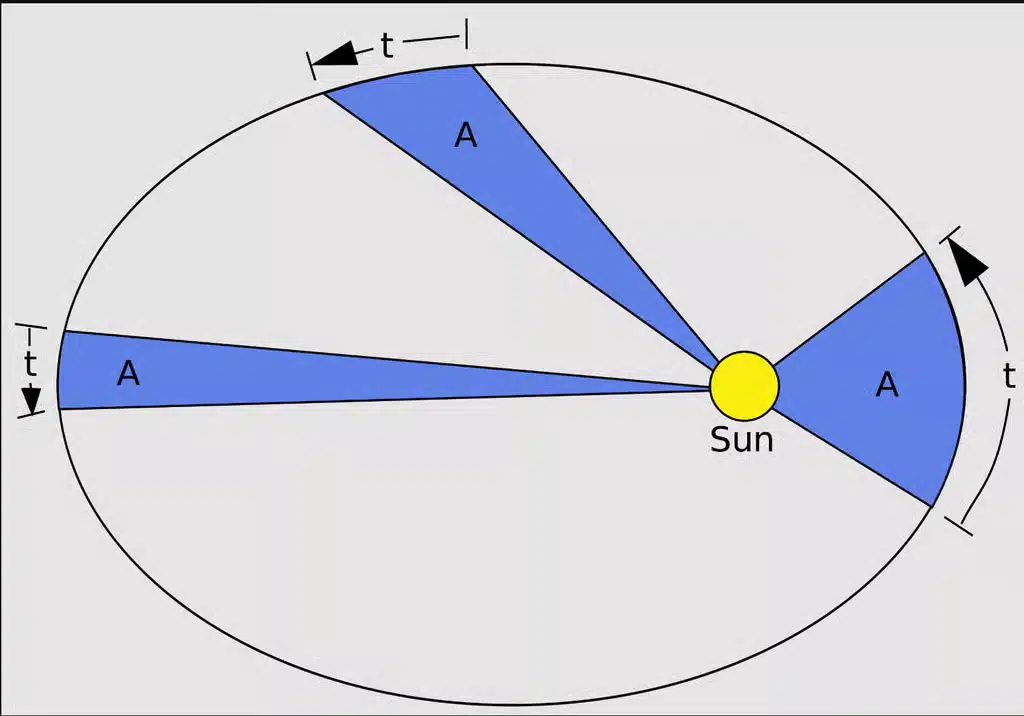
Interprétation géométrique : loi des aires

L’aire balayée par le rayon [math]r[/math] en un temps [math]\Delta t[/math] est :

\Delta A = \dfrac{1}{2} r \cdot v_t \cdot \Delta t.

Comme [math]r\cdot v_t[/math] est constant, on a :

\dfrac{\Delta A}{\Delta t} = \text{constante}.

Autrement dit, la planète balaie des aires égales en des temps égaux → c’est exactement la deuxième loi de Kepler.

III. Réflexions et prolongements

1. La situation actuelle

Aujourd’hui encore, les femmes restent minoritaires dans la recherche mathématique : on compte beaucoup moins de professeures ou de chercheuses que d’hommes dans les laboratoires et les universités. Mais la tendance évolue : les femmes sont de plus en plus nombreuses dans l’enseignement, dans la vulgarisation scientifique, et aussi dans des domaines appliqués très actuels comme la data science ou l’informatique théorique. Leur présence rend la discipline plus visible et plus accessible aux jeunes générations.

2. Une ouverture vers l’avenir

Une figure emblématique de ce progrès est Maryam Mirzakhani, première femme à recevoir la médaille Fields en 2014, la plus haute distinction en mathématiques. Ses travaux sur les surfaces de Riemann et la géométrie hyperbolique ont ouvert de nouvelles voies de recherche, et son parcours reste une source d’inspiration dans le monde entier.

Cette reconnaissance met en lumière un enjeu plus large : l’importance de la diversité en mathématiques. Plus de points de vue, plus de manières de penser, cela signifie aussi plus de créativité et de découvertes possibles.

Conclusion

Les femmes ont dû se battre pour trouver leur place en mathématiques, mais leurs découvertes montrent que cette science est universelle et qu’elle s’enrichit de toutes et de tous.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !