Comment les mathématiques permettent-elles de modéliser un phénomène périodique ?

Introduction

Les phénomènes périodiques sont partout autour de nous : le jour et la nuit, les saisons, les vibrations d’une corde. Pour les décrire et les comprendre, les mathématiques offrent de nombreux outils.

I. Comprendre la périodicité en mathématiques

1. Définition de la périodicité et exemples développés

On dit qu’une fonction [math]f[/math] est périodique s’il existe un réel [math]T > 0[/math] tel que :

f(x+T) = f(x) \quad \text{pour tout } x.

Le nombre [math]T[/math] est appelé une période de la fonction.

Exemples :

• [math]f(x) = \sin(x)[/math] vérifie [math]\sin(x+2\pi) = \sin(x)[/math], donc [math]2\pi[/math] est une période.
• [math]f(x) = \tan(x)[/math] est périodique de période [math]\pi[/math].
• Un pendule simple effectue un mouvement qui se répète toutes les [math]T = 2\pi \sqrt{\tfrac{L}{g}}[/math] secondes (avec [math]L[/math] la longueur, [math]g[/math] la gravité). On a donc une périodicité temporelle.

La périodicité traduit l’idée d’un phénomène qui revient à l’identique après un certain intervalle. C’est la base pour modéliser des mouvements cycliques, des saisons, des signaux électriques ou encore des ondes sonores.

2. Propriétés générales des fonctions périodiques

Au-delà des sinus et cosinus, toutes les fonctions périodiques partagent certaines propriétés mathématiques intéressantes.

• Symétrie et invariance
  Si [math]f[/math] est périodique de période [math]T[/math], alors elle a aussi pour période [math]kT[/math] pour tout entier [math]k \geq 1[/math].
  Exemple : [math]\sin(x)[/math] est de période [math]2\pi[/math], mais aussi [math]4\pi[/math], [math]6\pi[/math], etc.
• Moyenne sur une période
  On peut définir la valeur moyenne d’une fonction périodique sur une période :

\overline{f} = \tfrac{1}{T} \int_0^T f(x)dx.

Exemple :

\overline{\sin(x)} = \tfrac{1}{2\pi}\int_0^{2\pi}\sin(x)dx = 0.

Cette idée est utilisée en physique pour décrire des grandeurs «moyennes» comme la tension efficace en électricité.

II. Décomposer et analyser les phénomènes périodiques

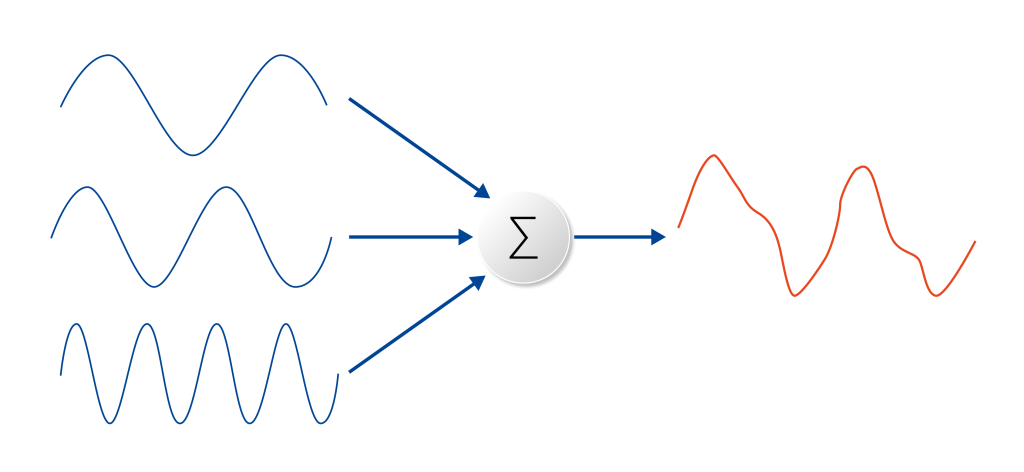
1. Superposition de signaux (principe de Fourier)

Jusqu’ici, nous avons vu que les fonctions sinus et cosinus permettent de modéliser des phénomènes simples comme un pendule ou une oscillation. Mais dans la réalité, de nombreux phénomènes périodiques sont beaucoup plus complexes : bruit, signaux électriques, ondes sonores…

Le mathématicien Joseph Fourier (1768–1830) a montré qu’on pouvait représenter tout signal périodique comme une combinaison de sinus et de cosinus de fréquences multiples.

Formellement, si [math]f(t)[/math] est une fonction périodique de période [math]T[/math], alors elle peut s’écrire sous la forme :

f(t) = a_0 + \sum_{n=1}^{\infty} \big( a_n \cos(n\omega t) + b_n \sin(n\omega t) \big),

où :

• [math]\omega = \tfrac{2\pi}{T}[/math] est la pulsation fondamentale,
• [math]a_n, b_n[/math] sont des coefficients appelés coefficients de Fourier, qui dépendent de la fonction étudiée.

Exemple concret : l’onde carrée

Une onde carrée est un signal qui alterne entre +1 et –1 à intervalles réguliers. Ce signal n’est pas une sinusoïde, et pourtant Fourier montre qu’il peut s’écrire comme une somme infinie de sinusoïdes :

f(t) = \tfrac{4}{\pi} \left( \sin(\omega t) + \tfrac{1}{3}\sin(3\omega t) + \tfrac{1}{5}\sin(5\omega t) + \cdots \right).

• Si on ne garde que [math]\sin(\omega t)[/math], on obtient une simple sinusoïde.
• En ajoutant [math]\sin(3\omega t)[/math] et [math]\sin(5\omega t)[/math], la fonction commence déjà à ressembler à une onde carrée.
• Plus on ajoute de termes, plus l’approximation devient précise.

2. Fréquences et spectre

Une autre manière de voir la série de Fourier est de dire que chaque signal périodique est composé de fréquences élémentaires.

• La fréquence fondamentale correspond à la période du signal,
• Les harmoniques (fréquences multiples) enrichissent le signal et lui donnent sa forme particulière.

On parle alors de spectre d’un signal : c’est la liste des fréquences qui le composent et de leur intensité.

Applications concrètes :

• Musique 🎵 :
  Un son émis par un instrument n’est jamais une sinusoïde pure. Par exemple, la note « La » à 440 Hz correspond à la fréquence fondamentale. Mais les harmoniques (880 Hz, 1320 Hz, etc.) définissent le timbre de l’instrument. Grâce à Fourier, on peut analyser un son et savoir s’il vient d’un violon, d’une flûte ou d’un piano.
• Électricité ⚡ :
  Dans un courant alternatif, si le signal est parfaitement sinusoïdal, il n’y a qu’une seule fréquence. Mais si le signal est déformé (parasites, distorsions), alors des harmoniques apparaissent. L’analyse de Fourier permet de détecter ces perturbations.
• Physique en général :
  Un phénomène périodique peut être vu soit dans le domaine du temps (oscillations successives), soit dans le domaine des fréquences (spectre obtenu grâce à Fourier).

III. Applications concrètes des modèles périodiques

1. Phénomènes naturels

Les mathématiques de la périodicité ne sont pas seulement théoriques : elles servent à comprendre des phénomènes essentiels de la nature.

Exemple : les marées 🌊

Les marées sont provoquées par l’attraction gravitationnelle de la Lune et du Soleil sur les océans.

• L’influence de la Lune crée une variation principale d’environ 12h25 (demi-journée lunaire).
• L’influence du Soleil ajoute une variation de période 12h.

Pour modéliser cela, on utilise la superposition de sinusoïdes :

h(t) = A_1 \sin\left(\tfrac{2\pi}{12,25}t\right) + A_2 \sin\left(\tfrac{2\pi}{12}t\right),

où [math]h(t)[/math] représente la hauteur de la mer à l’instant [math]t[/math], et [math]A_1, A_2[/math] les amplitudes des effets lunaire et solaire.

Résultat : la combinaison de ces deux sinusoïdes explique pourquoi certaines marées sont vives-eaux (grandes marées, quand les effets se renforcent) et d’autres mortes-eaux (faibles marées, quand les effets se compensent).

Exemple numérique : si [math]A_1 = 3[/math] m et [math]A_2 = 1[/math] m, alors la hauteur de marée varie entre 2 m et 4 m, selon l’interférence des deux ondes.

2. Phénomènes technologiques

Les sciences et technologies modernes reposent elles aussi sur la périodicité et son analyse.

Exemple : le son et sa compression 🎵

Un son est une vibration de l’air, donc une fonction périodique en temps (pression qui varie autour d’une valeur moyenne).

Si l’on enregistre une note de musique, elle n’est pas une sinusoïde parfaite : elle contient une fréquence fondamentale (la note) et plusieurs harmoniques (le timbre).

Grâce à la transformée de Fourier discrète, utilisée en informatique, on peut décomposer le son en fréquences et ne conserver que les plus importantes.

C’est le principe de la compression MP3 :

• On applique un algorithme de Fourier sur le signal sonore,
• On élimine les fréquences que l’oreille humaine perçoit mal,
• On ne garde que l’essentiel, ce qui réduit la taille du fichier.

Ainsi, un fichier audio brut (WAV) peut peser 50 Mo, mais compressé en MP3 grâce à Fourier, il tombe à 5 Mo, tout en gardant une qualité quasi identique. De la même façon, en imagerie numérique, la compression JPEG repose sur la décomposition des images en fréquences spatiales (zones uniformes ou variations rapides des couleurs).

Conclusion

Les mathématiques permettent donc de transformer les phénomènes périodiques en modèles prévisibles.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !