Comment les mathématiques permettent-elles de modéliser l’évolution d’une épidémie ?

Introduction

Quand une épidémie apparaît, on a l’impression qu’elle se propage de manière imprévisible. Pourtant, les mathématiques permettent non seulement d’expliquer comment elle se diffuse, mais aussi d’anticiper son évolution et d’agir pour la contrôler.

I. Décrire la croissance d’une épidémie : modèles simples

1. La croissance exponentielle au début de l’épidémie

Lorsqu’une épidémie démarre, l’idée de base est simple : chaque personne malade en contamine d’autres.

On note [math]R_0[/math] le taux de reproduction de base : c’est le nombre moyen de personnes contaminées par un seul malade.

• Si [math]R_0 = 1[/math], l’épidémie stagne.
• Si [math]R_0 < 1[/math], elle finit par disparaître.
• Si [math]R_0 > 1[/math], elle explose.

On peut alors écrire une formule pour le nombre de malades après [math]n[/math] «générations» d’infection :

M_n = M_0 \cdot R_0^n,

où [math]M_0[/math] est le nombre initial de malades.

En temps continu, cela se traduit par une fonction exponentielle :

M(t) = M_0 e^{rt},

où [math]r[/math] est lié à la vitesse de propagation.

Exemple : imaginons qu’au départ [math]M_0 = 10[/math] personnes soient infectées et que [math]R_0 = 2[/math].

• Après 1 génération : [math]M_1 = 20[/math].
• Après 2 générations : [math]M_2 = 40[/math].
• Après 5 générations : [math]M_5 = 10 \cdot 2^5 = 320[/math].

En seulement quelques étapes, le nombre de malades explose. C’est ce qu’on a observé lors des premières semaines du Covid-19 : les courbes de cas étaient exponentielles.

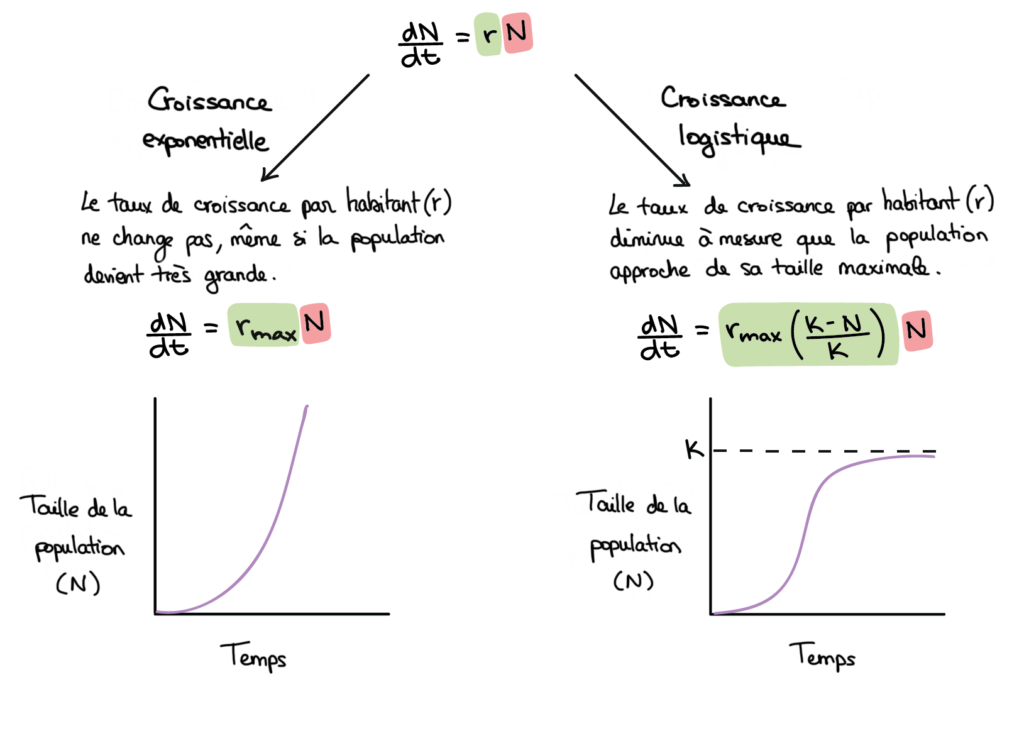
2. Le modèle logistique : quand la croissance ralentit

Le modèle exponentiel, aussi simple soit-il, a une limite : il suppose une population infinie et sans contraintes. Or, dans la réalité, une épidémie ne peut pas croître indéfiniment.

• Parce que la population totale est limitée.
• Parce qu’au fur et à mesure, beaucoup de personnes deviennent immunisées ou guérissent.
• Parce que les mesures sanitaires réduisent les contacts.

Pour tenir compte de cette réalité, on utilise le modèle logistique, qui ajoute une borne maximale [math]K[/math] correspondant à la taille totale de la population.

La formule est :

M(t) = \dfrac{K}{1 + A e^{-rt}},

où [math]A[/math] dépend du nombre initial de malades.

• Au début, le terme [math]e^{-rt}[/math] est grand, donc la croissance ressemble beaucoup à une exponentielle.
• Mais au fur et à mesure, [math]e^{-rt}[/math] devient petit, et [math]M(t)[/math] se rapproche de [math]K[/math].

Exemple : imaginons une petite ville de 1000 habitants ([math]K = 1000[/math]).

Même si au départ l’épidémie double très vite, elle ne pourra jamais dépasser [math]1000[/math] malades.

La courbe commence donc par monter rapidement, puis ralentit et finit par se stabiliser en formant une sigmoïde (forme en S).

Ce modèle a été utilisé par les épidémiologistes pour prévoir le nombre total de cas lors d’épidémies comme la grippe ou le Covid.

II. Probabilités et statistiques pour étudier la propagation

1. Probabilité d’infection et espérance de malades

Un contact entre une personne infectée et une personne saine peut être vu comme une épreuve de Bernoulli :

• avec probabilité [math]p[/math], la personne saine est contaminée ;
• avec probabilité [math]1-p[/math], elle reste saine.

Si [math]n[/math] personnes sont exposées, le nombre total de nouveaux malades [math]X[/math] suit une loi binomiale :

X \sim \mathcal{B}(n,p).

Cela signifie que la probabilité d’obtenir exactement [math]k[/math] contaminés est :

\mathbb{P}(X = k) = \binom{n}{k} p^k (1-p)^{n-k}.

L’espérance (la moyenne théorique attendue) vaut :

\mathbb{E}[X] = np.

Exemple : supposons que [math]n=100[/math] personnes soient en contact avec un malade, et que la probabilité de transmission soit [math]p=0{,}1[/math].

On obtient :

\mathbb{E}[X] = 100 \times 0{,}1 = 10.

Donc, en moyenne, 10 personnes seront contaminées.

Mais attention : ce n’est qu’une moyenne. En réalité, le nombre peut varier : par exemple, la probabilité qu’il y ait exactement 10 contaminés vaut [math]\mathbb{P}(X=10) = \binom{100}{10} (0{,}1)^{10} (0{,}9)^{90},[/math].

Ce modèle binomial permet de quantifier l’incertitude autour de la moyenne, et pas seulement de donner un chiffre unique.

2. Les statistiques pour estimer les paramètres d’un modèle

Dans les situations réelles, on ne connaît pas exactement la probabilité [math]p[/math] de contamination, ni même le [math]R_0[/math]. Ce sont des paramètres inconnus que l’on doit estimer à partir des données observées.

Exemple :

On observe que, sur [math]200[/math] personnes exposées, [math]50[/math] tombent malades.

On peut alors estimer [math]p[/math] par la fréquence observée :

\hat{p} = \frac{50}{200} = 0{,}25.

Mais cette estimation n’est pas parfaite : si on répétait l’expérience, on n’obtiendrait pas forcément le même résultat.

C’est pourquoi on utilise des intervalles de confiance, qui donnent une fourchette plausible pour la vraie valeur de [math]p[/math].

Par exemple, on pourrait conclure : «On estime que [math]p \approx 0{,}25[/math], avec une incertitude d’environ ±0,05.»

De la même manière, pour [math]R_0[/math], les épidémiologistes observent l’évolution du nombre de cas au cours du temps et ajustent un modèle exponentiel [math]M(t) = M_0 e^{rt}[/math] pour retrouver [math]r[/math], puis en déduire [math]R_0[/math].

III. Vers des modèles plus élaborés : le schéma SIR

1. Découper la population en compartiments

Le modèle SIR (Susceptibles – Infectés – Retirés) est l’un des plus célèbres en épidémiologie.

On partage la population en trois groupes :

• [math]S(t)[/math] : les personnes susceptibles d’être contaminées,
• [math]I(t)[/math] : les personnes infectées, capables de transmettre la maladie,
• [math]R(t)[/math] : les personnes retirées (soit guéries et immunisées, soit décédées).

On suppose que la population totale reste constante :

N = S(t) + I(t) + R(t).

La dynamique repose sur deux idées simples :

1. Plus il y a de contacts entre S et I, plus il y a de nouvelles infections.
   → Le nombre de susceptibles diminue selon : [math]\frac{dS}{dt} = -\beta S I. [/math] Ici, [math]\beta[/math] est le taux de transmission : il mesure la probabilité qu’un contact entre un malade et un sain entraîne une infection.
2. Les infectés guérissent (ou quittent la contagion) à un rythme proportionnel à leur nombre.
   → Le nombre de guérisons par unité de temps est [math]\gamma I[/math], où [math]\gamma[/math] est le taux de guérison.

Ainsi, le système complet est :

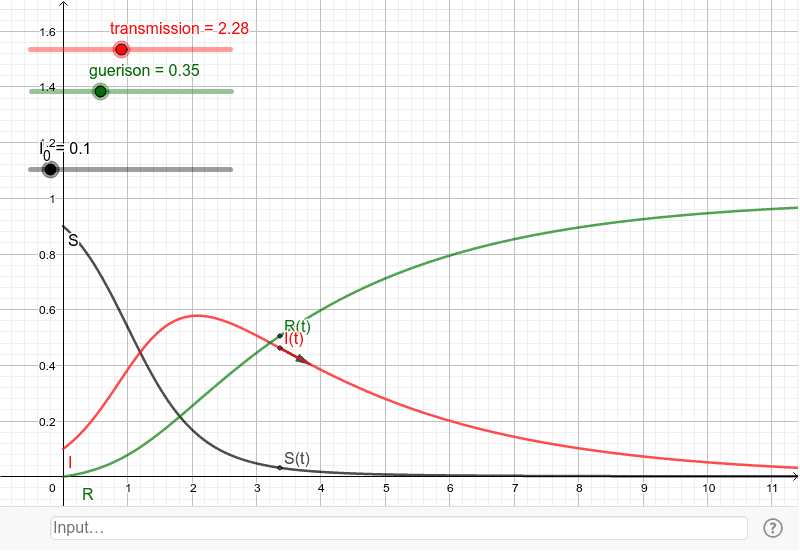
\frac{dS}{dt} = -\beta S I, \quad \frac{dI}{dt} = \beta S I - \gamma I, \quad \frac{dR}{dt} = \gamma I.

Même sans résoudre ce système, on peut comprendre qualitativement :

• au début, [math]I(t)[/math] croît très vite si beaucoup de personnes sont susceptibles,
• mais quand [math]S(t)[/math] diminue, les nouvelles infections ralentissent,
• finalement [math]I(t)[/math] redescend, et l’épidémie s’éteint.

Ce schéma explique pourquoi une épidémie suit souvent une courbe en cloche : croissance rapide, pic, puis déclin.

2. Le seuil épidémique et l’importance de [math]R_0[/math]

Un paramètre clé est le nombre de reproduction de base :

R_0 = \frac{\beta}{\gamma}.

• Si [math]R_0 > 1[/math] → chaque malade infecte en moyenne plus d’une personne → l’épidémie se propage.
• Si [math]R_0 < 1[/math] → chaque malade transmet la maladie à moins d’une personne en moyenne → l’épidémie s’éteint naturellement.

Exemple numérique :

• Si [math]\beta = 0{,}3[/math] et [math]\gamma = 0{,}1[/math], alors [math]R_0 = 3[/math]. Cela signifie qu’un malade contamine en moyenne 3 autres personnes → épidémie explosive.
• Si [math]\beta = 0{,}05[/math] et [math]\gamma = 0{,}1[/math], alors [math]R_0 = 0{,}5[/math]. Chaque malade contamine moins d’une personne → l’épidémie s’éteint rapidement.

Ce seuil permet de comprendre pourquoi les mesures de santé publique (vaccination, port du masque, confinement) cherchent à réduire [math]\beta[/math].

Par exemple, si une vaccination réduit le nombre de personnes susceptibles [math]S(t)[/math], le produit [math]\beta S I[/math] diminue, et l’épidémie est freinée.

Une conséquence importante est le concept d’immunité collective :

• pour qu’une épidémie ne se propage pas, il faut que la proportion de personnes immunisées dépasse [math]1 – \tfrac{1}{R_0}[/math].
• Exemple : si [math]R_0 = 3[/math], il faut immuniser au moins [math]1 – \tfrac{1}{3} = \tfrac{2}{3} = 66{,}7\%[/math] de la population pour bloquer l’épidémie.

Conclusion

Ces modèles permettent ainsi de mieux comprendre comment une épidémie démarre, comment elle se propage et surtout comment on peut l’arrêter.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !