Hôtel de Hilbert : l’infini en maths

Introduction
🛎️ Imaginez un hôtel avec une infinité de chambres… toutes occupées ! Que se passe-t-il si un nouveau client arrive ? Et si une infinité de clients, ou même une infinité de bus, veulent aussi une chambre ?
C’est le paradoxe de l’Hôtel de Hilbert, une expérience de pensée qui révèle à quel point l’infini peut réserver des surprises en mathématiques.
I. La première surprise de l’infini
1. Rappel de la définition d’une bijection
En mathématiques, une bijection est une fonction qui met en correspondance chaque élément d’un ensemble avec un et un seul élément d’un autre ensemble, et réciproquement.
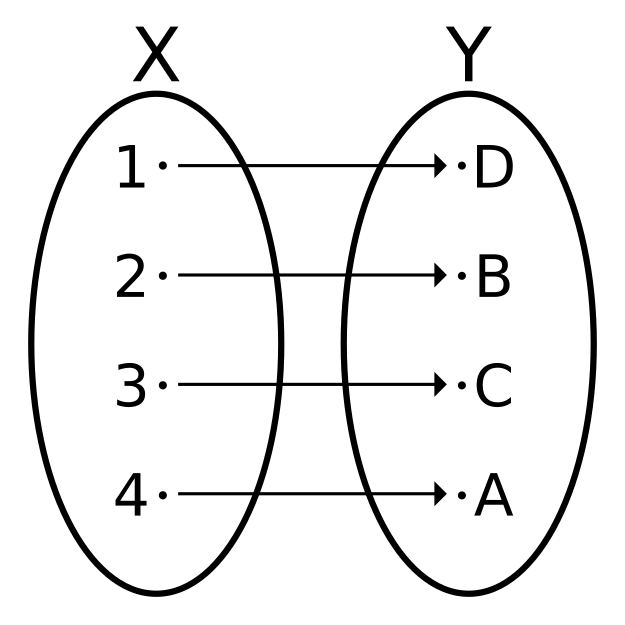
Autrement dit, personne n’est oublié, et personne n’a deux places : chaque élément d’un côté a exactement un partenaire de l’autre côté.
Un exemple simple est la fonction :
f(n) = n - 1.
- Ici, [math]f[/math] est définie de [math]\mathbb{N}^*[/math] (les entiers naturels non nuls, avec 1, 2, …) vers [math]\mathbb{N}[/math] (les entiers naturels, donc 0, 1, 2, 3, …).
- Si on commence à [math]n=1[/math], alors [math]f(1)=0[/math], [math]f(2)=1[/math], [math]f(3)=2[/math], etc.
En fait, on peut aussi considérer la fonction inverse :
g(n) = n + 1,
qui est une bijection de [math]\mathbb{N}[/math] vers [math]\mathbb{N}^*[/math].
2. Lien avec l’hôtel
Imaginons maintenant l’hôtel de Hilbert, un hôtel avec une infinité de chambres, toutes occupées.
Un nouveau client arrive : comment lui trouver une chambre ?
- On demande à chaque client de la chambre [math]n[/math] d’aller dans la chambre [math]n+1[/math].
- Ainsi, le client de la chambre 1 va dans la chambre 2, celui de la chambre 2 va dans la chambre 3, etc.
- Toutes les chambres restent occupées… sauf la chambre 1, qui se libère pour accueillir le nouveau client.
Ce simple décalage illustre bien l’idée qu’avec la bijection précédente, on peut toujours «faire de la place».
II. Quand une infinité de nouveaux clients arrive…
1. Stratégie 1 : multiplier par 2
Imaginons maintenant que toute une infinité de nouveaux clients se présente à l’hôtel, alors que toutes les chambres sont déjà occupées.
Une solution astucieuse est de demander à chaque client actuel de la chambre [math]n[/math] d’aller dans la chambre [math]2n[/math].
- Ainsi, le client de la chambre 1 va dans la chambre 2, celui de la chambre 2 va dans la chambre 4, celui de la chambre 3 va dans la chambre 6, etc.
- Toutes les chambres paires sont maintenant occupées.
- Par contre, toutes les chambres impaires (1, 3, 5, …) se sont libérées !
On peut donc loger l’infinité de nouveaux clients en leur donnant les chambres impaires, selon la règle :
i \mapsto 2i - 1
2. Stratégie 2 : une infinité de bus d’infinité de clients
Supposons maintenant qu’une infinité de bus arrive à l’hôtel, et que dans chaque bus il y ait une infinité de clients !
On peut noter le client [math]i[/math] du bus [math]j[/math] par la paire [math]i,j[/math].
Méthode 1 : avec les puissances de 2
On peut numéroter chaque client avec une formule comme :
i,j \mapsto 2^i \times (2j + 1)
Cela garantit que deux clients différents [math](i,j) \neq (i’,j’)[/math] ne tombent jamais dans la même chambre.
Supposons [math]2^{,i}(2j+1)=2^{,i’}(2j’+1)[/math].
En comparant la puissance de 2 (unicité de la décomposition en facteurs premiers), on obtient [math]i=i'[/math]. En simplifiant, [math]2j+1=2j’+1[/math], donc [math]j=j'[/math]. Ainsi, cette fonction est bijective. (en réalité, on a seulement montré l’injectivité, mais la surjectivité est assez simple à voir : elle repose sur le fait que tout entier pair peut s’écrire de façon unique comme une puissance de 2 multipliée par un impair. Voir ici pour plus de détails sur le vocabulaire, qui va un peu au-delà du programme de Terminale.).
Méthode 2 : le tableau à deux entrées
Une autre façon, plus pédagogique, est de construire un tableau infini :
- Chaque ligne correspond au numéro du client [math]i[/math].
- Chaque colonne correspond au numéro du bus [math]j[/math].
On obtient ainsi un tableau à deux entrées qui contient tous les clients possibles.
Ensuite, on peut parcourir ce tableau en suivant les diagonales (d’abord [math]1,1[/math], puis [math]1,2[/math], [math]2,1[/math], puis [math]1,3[/math], [math]2,2[/math], [math]3,1[/math], etc.).
| Bus 1 | Bus 2 | Bus 3 | Bus 4 | … | |
|---|---|---|---|---|---|
| Client 1 | (1,1) | (1,2) | (1,3) | (1,4) | … |
| Client 2 | (2,1) | (2,2) | (2,3) | (2,4) | … |
| Client 3 | (3,1) | (3,2) | (3,3) | (3,4) | … |
| Client 4 | (4,1) | (4,2) | (4,3) | (4,4) | … |
| … | … | … | … | … | … |
De cette manière, on construit une bijection :
\mathbb{N}^* \times \mathbb{N}^* \longleftrightarrow \mathbb{N}^*III. Tous les infinis se valent-ils ? L’argument de Cantor
1. L’exemple des menus infinis
Pour aller encore plus loin, prenons un exemple différent : imaginons un restaurant avec une infinité de plats possibles.
Un repas complet correspond alors à une suite infinie de plats (entrée, plat principal, dessert, boisson, etc. à l’infini).
On peut représenter cette situation par un tableau :
- Chaque ligne du tableau correspond à un client (c’est-à-dire un repas).
- Chaque colonne correspond à la position dans le menu (premier plat, deuxième plat, troisième plat, etc.).
Maintenant, grâce à la célèbre méthode de la diagonale de Cantor, on peut montrer qu’il existe toujours un repas qui n’est pas encore dans la liste :
- Pour le 1er plat, on choisit un plat différent de celui du 1er client.
- Pour le 2e plat, on choisit un plat différent de celui du 2e client.
- Pour le 3e plat, on choisit un plat différent de celui du 3e client.
- Et ainsi de suite…
On obtient un nouveau repas qui diffère de tous les autres au moins à une position.
2. Interprétation mathématique
Ce phénomène a été étudié par le mathématicien Georg Cantor.
- L’ensemble [math]\mathbb{N}[/math] (les entiers naturels) est un infini dit dénombrable : on peut compter ses éléments un par un.
- Mais l’ensemble des suites infinies (par exemple toutes les suites de 0 et de 1) est un infini non dénombrable : il est strictement plus grand que [math]\mathbb{N}[/math].
- De même, l’ensemble des nombres réels [math]\mathbb{R}[/math] est un infini plus grand que celui des entiers.
Conclusion
L’Hôtel de Hilbert montre que l’infini ne se comporte pas comme les nombres «classiques» : on peut toujours faire de la place pour plus de clients, même quand l’hôtel peut sembler plein. Mais grâce à Cantor, on découvre qu’il existe en réalité plusieurs tailles d’infini… ce qui rend ce concept encore plus fascinant !
On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !








