Cryptomonnaies : l’exemple du Bitcoin

Introduction
Le Bitcoin est la première cryptomonnaie, créée en 2009, et il fascine autant qu’il intrigue. Contrairement à une monnaie classique émise par une banque centrale, sa création repose sur un protocole mathématique précis, qui garantit une rareté programmée : au maximum 21 millions de bitcoins seront créés, et pas un de plus.
Ce mécanisme pose une question intéressante de mathématiques : comment modéliser la quantité de bitcoins en circulation au fil du temps ?

I. Le mécanisme d’émission du Bitcoin
1. Création par cycles de 4 ans (les « halvings »)
Le Bitcoin (2009, Satoshi Nakamoto) émet de nouvelles unités en rémunérant les mineurs qui valident des blocs. Cette récompense par bloc est divisée par 2 tous les 210 000 blocs (≈ 4 ans) : on parle de halving.
Au départ, la récompense valait 50 BTC par bloc, puis 25, 12.5, 6.25, etc. (on divise par 2 à chaque cycle).
Comme il y a [math]210000[/math] blocs par cycle, la quantité créée à chaque cycle suit une suite géométrique :
- Cycle 1 (2009–2012) : [math]210000 \times 50 = 10500000[/math] BTC [math]= 10.5[/math] millions
- Cycle 2 (2012–2016) : [math]210000 \times 25 = 5250000[/math] BTC [math]= 5.25[/math] millions
- Cycle 3 (2016–2020) : [math]210000 \times 12.5 = 2625000[/math] BTC [math]= 2.625[/math] millions
- etc. (à chaque cycle on divise par 2)
Visuellement, c’est une « exponentielle inversée » : on ajoute d’abord beaucoup, puis deux fois moins, puis encore deux fois moins… On se rapproche d’une limite.
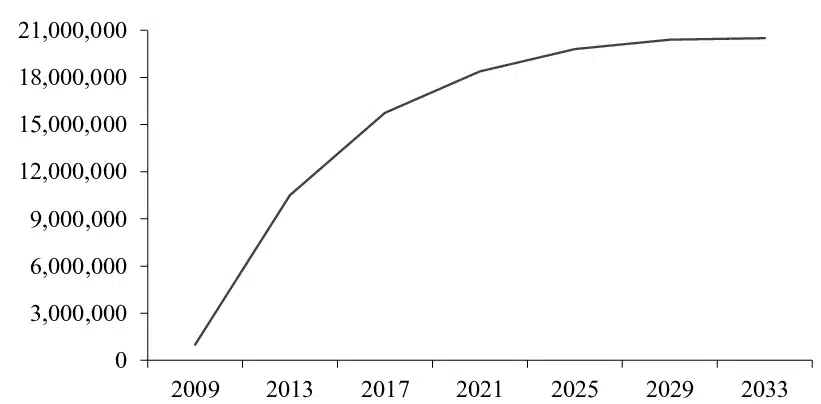
2. Modélisation par une suite et somme télescopique
Notons :
- [math]u_n[/math] : total de bitcoins créés après [math]n[/math] cycles (en millions de BTC),
- [math]v_n = u_{n+1}-u_n[/math] : création pendant le cycle [math]n[/math] (en millions).
Avec notre comptage, on a :
- [math]u_0 = 0[/math] (avant tout début, total créé nul),
- [math]v_0 = 10.5,\ v_1 = 5.25,\ v_2 = 2.625,\ \dots[/math]
donc [math]v_n = \dfrac{21}{2^{n+1}}[/math] (en millions), car [math]10.5 = \dfrac{21}{2}[/math], [math]5.25 = \dfrac{21}{4}[/math], etc.
Comme [math]u_n[/math] est la somme des créations jusqu’au cycle [math]n-1[/math], on écrit la somme télescopique standard :
\underbrace{(u_1 - u_0)}_{v_0} + \underbrace{(u_2 - u_1)}_{v_1} + \cdots + \underbrace{(u_n - u_{n-1})}_{v_{n-1}} = u_n - u_0 = u_nDonc
u_n = \sum_{k=0}^{n-1} v_k = \sum_{k=0}^{n-1} \frac{21}{2^{k+1}} = 21 \sum_{k=0}^{n-1} \frac{1}{2^{k+1}}Or
\sum_{k=0}^{n-1} \frac{1}{2^{k+1}}
= \frac{1}{2}\left(1 + \frac{1}{2} + \cdots + \frac{1}{2^{n-1}}\right)
= 1 - \frac{1}{2^{n}}.Ainsi, on obtient la formule fermée (en millions de BTC) :
u_n = 21\left(1 - \frac{1}{2^{n}}\right).Vérifications rapides :
- [math]u_1 = 21(1-\tfrac{1}{2})=10.5[/math] (ok),
- [math]u_2 = 21(1-\tfrac{1}{4})=15.75[/math] (10.5 + 5.25),
- [math]u_3 = 21(1-\tfrac{1}{8})=18.375[/math] (15.75 + 2.625), etc.
Après [math]n[/math] cycles, on a déjà créé une part [math]1 – \tfrac{1}{2^n}[/math] de la limite [math]21[/math] (millions). Chaque cycle ajoute [math]v_n = \dfrac{21}{2^{n+1}}[/math] (millions), c’est-à-dire deux fois moins que le précédent.
II. Limite et asymptote des 21 millions
1. Calcul de la limite de la suite
On rappelle que la suite du nombre total de bitcoins créés après [math]n[/math] cycles de 4 ans est donnée par :
u_n = 21\left(1-\tfrac{1}{2^n}\right).Quand [math]n \to \infty[/math], le terme [math]\tfrac{1}{2^n}[/math] tend vers 0.
Donc :
\lim_{n\to\infty} u_n = 21(1-0) = 21.➡ Cela signifie que le protocole du Bitcoin impose une borne supérieure de 21 millions.
2. Quand le dernier bitcoin sera-t-il miné ?
À chaque cycle, la récompense est divisée par 2. Il reste donc une infinité de cycles à parcourir, mais les quantités ajoutées deviennent de plus en plus petites.
Ici, on veut quantifier « presque 21 millions« .
Comme on a défini [math]u_n[/math] en millions de BTC, écrire [math]u_n = 20{,}999999[/math] signifie qu’il reste [math]21 – 20{,}999999 = 0{,}000001[/math] million de BTC, soit 1 BTC à émettre.
On résout donc, avec [math]u_n = 21\left(1-\tfrac{1}{2^n}\right)[/math] :
21\left(1-\tfrac{1}{2^n}\right) = 20{,}999999 \Longleftrightarrow \tfrac{1}{2^n} = \tfrac{0{,}000001}{21} \Longleftrightarrow n = \log_2\!\big(\tfrac{21}{10^{-6}}\big) = \log_2(21\times 10^6) \approx 24{,}32.Un cycle dure ~4 ans, donc l’année correspondante est environ
2009 + 4\times 24{,}32 \approx 2009 + 4\times 24 = 2105.Aux alentours de 2105 (après 24 cycles), il ne resterait plus qu’environ 1 bitcoin à créer : on serait quasiment à la limite des 21 millions, mais il subsisterait encore des fractions à émettre.
3. La limite pratique : le satoshi
En pratique, on ne peut pas aller en dessous du satoshi, la plus petite unité de bitcoin :La plus petite unité est le satoshi : [math]1\ \text{satoshi} = 10^{-8}\ \text{BTC}.[/math]
Après [math]i[/math] halvings, la récompense par bloc vaut [math]\dfrac{50}{2^i}[/math] BTC. L’émission «s’arrête» en pratique dès que cette récompense devient strictement inférieure à 1 satoshi :
\frac{50}{2^i} < 10^{-8} \Longleftrightarrow 2^i > 5\times 10^9 \Longleftrightarrow i > \log_2(5\times 10^9) \approx 32{,}22.Le plus petit entier est donc [math]i=33[/math].
Avec ~4 ans par halving, cela donne [math]2009 + 4\times 33 \approx 2141.[/math]
Conclusion
- Le protocole du Bitcoin repose sur une suite géométrique convergente, qui garantit que le nombre total n’excédera jamais 21 millions.
- Cette rareté programmée, appuyée par les mathématiques, explique pourquoi le Bitcoin est souvent considéré comme une sorte « d’or numérique ».
On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !








