Les Fractales : l’exemple du flocon de Koch

Introduction

Le flocon de Koch est une figure géométrique étonnante : en partant simplement d’un triangle équilatéral et en répétant toujours la même règle de construction, on obtient une courbe avec des propriétés assez surprenantes.

Elle fait partie des fractales, ces objets mathématiques très complexes, pourtant souvent construit à partir de règles simples.

Dans ce sujet, nous allons voir comment se construit le flocon, pourquoi son périmètre devient infini, et pourtant pourquoi son aire reste finie.

I. Construction du flocon de Koch

1. Définition et premières étapes

On part d’un triangle équilatéral de côté [math]a[/math]. Appelons étape 0 cette figure initiale.

Règle de construction (même à chaque étape)

Sur chaque côté existant :

1. On partage le segment en trois parties égales.
2. On retire le tiers central.
3. À sa place, on érige un petit triangle équilatéral tourné vers l’extérieur (de sorte que la figure reste « en dents de scie »).

Conséquence sur un seul segment de longueur [math]L[/math] :

• il est remplacé par 4 segments,
• chacun de longueur [math]\tfrac{L}{3}[/math].

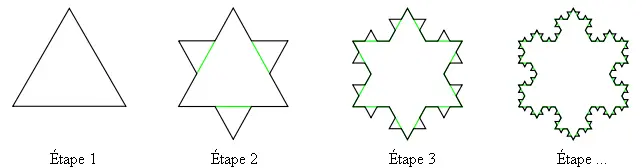
Illustration sur les premières étapes (idée) :

• Étape 0 : un triangle → 3 côtés de longueur [math]a[/math].
• Étape 1 : chaque côté donne 4 segments de longueur [math]\tfrac{a}{3}[/math] → la figure a 12 côtés.
• Étape 2 : chaque côté (long [math]\tfrac{a}{3}[/math]) est à son tour remplacé par 4 segments de longueur [math]\tfrac{a}{9}[/math], etc.

Voici une petite vidéo pour voir en pratique comment procéder pour les première étapes : (à savoir refaire !)

2. Nombre de côtés et longueur d’un côté

Notons :

• [math]C_n[/math] = nombre de côtés à l’étape [math]n[/math] ;
• [math]l_n[/math] = longueur d’un côté à l’étape [math]n[/math].

a. Formule pour [math]C_n[/math]

• À l’étape 0 : [math]C_0 = 3[/math] (le triangle initial).
• Une étape remplace chaque côté par 4 nouveaux côtés. Donc :
  [math]C_{n+1} = 4,C_n.[/math]

Cette relation de récurrence (suite géométrique de raison 4) se résout immédiatement :

C_n = 3 \cdot 4^n.

Vérification rapide :

• [math]n=1[/math] : [math]C_1 = 3\cdot 4 = 12[/math] (OK).
• [math]n=2[/math] : [math]C_2 = 3\cdot 4^2 = 48[/math] (OK).

b. Formule pour [math]l_n[/math]

• À l’étape 0 : [math]l_0 = a[/math].
• À chaque étape, la longueur de chaque côté est divisée par 3 (chaque segment est remplacé par 4 segments, chacun long d’un tiers). Donc : [math]l_{n+1} = \tfrac{1}{3}l_n.[/math]

C’est encore une suite géométrique (raison [math]\tfrac{1}{3}[/math]) :

l_n = a \cdot \left(\tfrac{1}{3}\right)^n.

Vérification rapide :

[math]n=3[/math] : [math]l_3 = a/27[/math], etc.

[math]n=1[/math] : [math]l_1 = a/3[/math].

[math]n=2[/math] : [math]l_2 = a/9[/math].

II. Le périmètre du flocon

1. Expression du périmètre

On rappelle les résultats de la partie I :

• [math]C_n = 3 \cdot 4^n[/math] (nombre de côtés à l’étape [math]n[/math]),
• [math]l_n = a \cdot \left(\tfrac{1}{3}\right)^n[/math] (longueur d’un côté).

Le périmètre à l’étape [math]n[/math] est donc :

P_n = C_n \cdot l_n.

En remplaçant :

P_n = \big(3 \cdot 4^n\big) \times \Big(a \cdot \big(\tfrac{1}{3}\big)^n\Big).

P_n = 3a \cdot \left(\tfrac{4}{3}\right)^n.