Les Fractales : l’exemple du flocon de Koch

Introduction

Le flocon de Koch est une figure géométrique étonnante : en partant simplement d’un triangle équilatéral et en répétant toujours la même règle de construction, on obtient une courbe avec des propriétés assez surprenantes.

Elle fait partie des fractales, ces objets mathématiques très complexes, pourtant souvent construit à partir de règles simples.

Dans ce sujet, nous allons voir comment se construit le flocon, pourquoi son périmètre devient infini, et pourtant pourquoi son aire reste finie.

I. Construction du flocon de Koch

1. Définition et premières étapes

On part d’un triangle équilatéral de côté [math]a[/math]. Appelons étape 0 cette figure initiale.

Règle de construction (même à chaque étape)

Sur chaque côté existant :

1. On partage le segment en trois parties égales.
2. On retire le tiers central.
3. À sa place, on érige un petit triangle équilatéral tourné vers l’extérieur (de sorte que la figure reste « en dents de scie »).

Conséquence sur un seul segment de longueur [math]L[/math] :

• il est remplacé par 4 segments,
• chacun de longueur [math]\tfrac{L}{3}[/math].

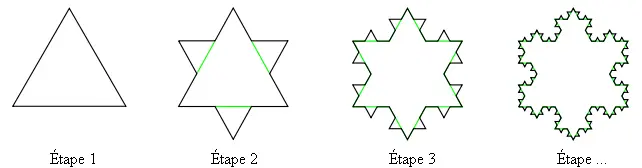
Illustration sur les premières étapes (idée) :

• Étape 0 : un triangle → 3 côtés de longueur [math]a[/math].
• Étape 1 : chaque côté donne 4 segments de longueur [math]\tfrac{a}{3}[/math] → la figure a 12 côtés.
• Étape 2 : chaque côté (long [math]\tfrac{a}{3}[/math]) est à son tour remplacé par 4 segments de longueur [math]\tfrac{a}{9}[/math], etc.

Voici une petite vidéo pour voir en pratique comment procéder pour les première étapes : (à savoir refaire !)

2. Nombre de côtés et longueur d’un côté

Notons :

• [math]C_n[/math] = nombre de côtés à l’étape [math]n[/math] ;
• [math]l_n[/math] = longueur d’un côté à l’étape [math]n[/math].

a. Formule pour [math]C_n[/math]

• À l’étape 0 : [math]C_0 = 3[/math] (le triangle initial).
• Une étape remplace chaque côté par 4 nouveaux côtés. Donc :
  [math]C_{n+1} = 4,C_n.[/math]

Cette relation de récurrence (suite géométrique de raison 4) se résout immédiatement :

C_n = 3 \cdot 4^n.

Vérification rapide :

• [math]n=1[/math] : [math]C_1 = 3\cdot 4 = 12[/math] (OK).
• [math]n=2[/math] : [math]C_2 = 3\cdot 4^2 = 48[/math] (OK).

b. Formule pour [math]l_n[/math]

• À l’étape 0 : [math]l_0 = a[/math].
• À chaque étape, la longueur de chaque côté est divisée par 3 (chaque segment est remplacé par 4 segments, chacun long d’un tiers). Donc : [math]l_{n+1} = \tfrac{1}{3}l_n.[/math]

C’est encore une suite géométrique (raison [math]\tfrac{1}{3}[/math]) :

l_n = a \cdot \left(\tfrac{1}{3}\right)^n.

Vérification rapide :

[math]n=3[/math] : [math]l_3 = a/27[/math], etc.

[math]n=1[/math] : [math]l_1 = a/3[/math].

[math]n=2[/math] : [math]l_2 = a/9[/math].

II. Le périmètre du flocon

1. Expression du périmètre

On rappelle les résultats de la partie I :

• [math]C_n = 3 \cdot 4^n[/math] (nombre de côtés à l’étape [math]n[/math]),
• [math]l_n = a \cdot \left(\tfrac{1}{3}\right)^n[/math] (longueur d’un côté).

Le périmètre à l’étape [math]n[/math] est donc :

P_n = C_n \cdot l_n.

En remplaçant :

P_n = \big(3 \cdot 4^n\big) \times \Big(a \cdot \big(\tfrac{1}{3}\big)^n\Big).

P_n = 3a \cdot \left(\tfrac{4}{3}\right)^n.

2. Conséquence : un périmètre infini

Comme [math]\tfrac{4}{3} > 1[/math], la suite [math]P_n[/math] croît indéfiniment :

P_n = 3a \cdot \left(\tfrac{4}{3}\right)^n \xrightarrow[n\to\infty]{} +\infty.

Lecture intuitive :

• À chaque étape, le périmètre est multiplié par [math]\tfrac{4}{3}[/math] (augmentation de +33%).
• L’accroissement est donné par :

P_{n+1} - P_n = \left(\tfrac{4}{3}-1\right)P_n = \tfrac{1}{3}P_n > 0.

Exemple numérique (avec [math]a=1[/math]) :

• [math]P_0 = 3[/math]
• [math]P_1 = 4[/math]
• [math]P_2 = \tfrac{16}{3} \approx 5,33[/math]
• [math]P_3 = \tfrac{64}{9} \approx 7,11[/math]
• … et ainsi de suite, sans borne supérieure.

III. L’aire du flocon

1. Aire d’un triangle équilatéral (rappel)

On trace la hauteur depuis un sommet. Elle coupe la base en son milieu et forme deux triangles rectangles isocèles avec un angle de [math]60^\circ[/math] au sommet.

• La moitié de la base vaut [math]\tfrac{a}{2}[/math].
• Notons [math]h[/math] la hauteur. Dans le triangle rectangle, on a [math]\tan 60^\circ = \tfrac{h}{a/2} \Rightarrow h = \tfrac{a}{2}\tan 60^\circ = \tfrac{a}{2}\sqrt{3} = \tfrac{\sqrt{3}}{2}a[/math].

L’aire du triangle vaut alors :

A = \tfrac{1}{2} \times \text{base} \times \text{hauteur} = \tfrac{1}{2} \times a \times \tfrac{\sqrt{3}}{2}a = \tfrac{\sqrt{3}}{4}a^2.

Donc, à l’étape 0 (triangle initial du flocon) :

A_0 = \tfrac{\sqrt{3}}{4}a^2.

2. Une infinité d’ajouts… pour une aire finie !

À l’étape n → n+1, sur chaque côté de longueur [math]l_n[/math], on ajoute un petit triangle équilatéral dont le côté est le tiers du côté de départ, donc [math]\tfrac{l_n}{3}[/math].

L’aire ajoutée par un côté vaut alors :

\tfrac{\sqrt{3}}{4}\left(\tfrac{l_n}{3}\right)^2=\tfrac{\sqrt{3}}{36}l_n^2.

Comme il y a [math]C_n[/math] côtés à l’étape [math]n[/math], l’accroissement d’aire est :

A_{n+1}-A_n=C_n\cdot\tfrac{\sqrt{3}}{36}l_n^2.

On remplace par les expressions trouvées en partie I :

C_n=3\cdot 4^n,\qquad l_n=a\left(\tfrac{1}{3}\right)^n.

Ainsi,

\begin{aligned}
A_{n+1}-A_n
&= \left(3\cdot 4^n\right)\cdot\tfrac{\sqrt{3}}{36}\cdot
\left(a^2\left(\tfrac{1}{3}\right)^{2n}\right) \
&= \tfrac{\sqrt{3}a^2}{12}\left(\tfrac{4}{9}\right)^n
\end{aligned}.

C’est une suite géométrique de raison [math]\tfrac{4}{9}<1[/math].

On peut alors calculer l’aire totale à l’étape [math]m[/math] en additionnant tous les accroissements :

A_m = A_0 + \sum_{k=0}^{m-1} (A_{k+1}-A_k).

Comme il s’agit d’une somme télescopique, cette formule revient à additionner directement les aires ajoutées à chaque étape.

En utilisant l’expression trouvée pour [math]A_{n+1}-A_n[/math], on obtient :

A_m = A_0 + \sum_{k=0}^{m-1} \tfrac{\sqrt{3}a^2}{12}\left(\tfrac{4}{9}\right)^k.

C’est une somme géométrique de raison [math]\tfrac{4}{9}[/math]. Sa valeur exacte est :

A_m = A_0 + \tfrac{\sqrt{3}a^2}{12} \cdot \frac{1 - \left(\tfrac{4}{9}\right)^m}{1 - \tfrac{4}{9}}.

Quand [math]m \to \infty[/math], le terme [math]\left(\tfrac{4}{9}\right)^m[/math] tend vers 0. On trouve alors :

A_\infty = A_0 + \tfrac{\sqrt{3}a^2}{12} \cdot \frac{1}{1 - \tfrac{4}{9}}
= A_0 + \tfrac{3\sqrt{3}}{20}a^2.

Or [math]A_0 = \tfrac{\sqrt{3}}{4}a^2[/math], donc au final :

A_\infty = \tfrac{2\sqrt{3}}{5}a^2 = \tfrac{8}{5}A_0.

Conclusion

Le flocon de Koch est un bel exemple de fractale : son périmètre devient infini alors que son aire reste finie. Cela montre comment, à partir d’une règle géométrique très simple, on obtient une figure aux propriétés surprenantes.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !