Peut-on éviter les embouteillages grâce aux mathématiques ?

Introduction

Chaque matin ou chaque soir, des millions d’automobilistes se retrouvent coincés dans les embouteillages. Perte de temps, pollution, stress… c’est un vrai fléau. Pourtant, ce phénomène ne dépend pas seulement du hasard ou de la malchance : il obéit à des lois mathématiques.

En effet, derrière un simple ralentissement se cachent des notions de densité, de flux, de probabilités et même d’optimisation. Mieux encore, les mathématiques permettent de comprendre pourquoi certains bouchons apparaissent « sans raison », de modéliser la circulation comme un système, et d’imaginer des solutions pour les fluidifier.

La question est donc la suivante : peut-on éviter les embouteillages grâce aux mathématiques ?

Avant d’attaquer le sujet, voici une petite vidéo à visionner 🙂

I. Comprendre les embouteillages avec les maths du quotidien

1. Un problème de flux : densité et débit

Pour étudier la circulation, on peut la voir comme un « flux » de voitures, un peu comme l’eau qui s’écoule dans un tuyau.

Deux grandeurs mathématiques sont utiles :

• La densité de circulation : [math] \rho = \tfrac{N}{L} [/math].
  C’est le nombre de voitures [math]N[/math] présentes sur une portion de route de longueur [math]L[/math]. On l’exprime en voitures par kilomètre.
• Le débit de circulation : [math] q = \rho \cdot v [/math].
  C’est le nombre de voitures qui passent en un point de la route par unité de temps. Il dépend à la fois de la densité [math]\rho[/math] et de la vitesse moyenne [math]v[/math].

Exemple :

Si on a [math]\rho = 20[/math] voitures/km sur une autoroute, et que la vitesse moyenne est [math]v = 100[/math] km/h, alors le débit est : [math] q = 20 \times 100 = 2000 \text{ voitures/heure} [/math].

2. Les embouteillages « fantômes » : suites et propagation

Le plus étonnant, c’est qu’un embouteillage peut apparaître sans accident ni obstacle : ce sont les « bouchons fantômes ».

Imagine une file de voitures roulant à 100 km/h. Si une voiture freine légèrement, celle qui la suit freine un peu plus, puis la suivante encore davantage. Ce petit ralentissement se propage comme une onde vers l’arrière, et au bout de quelques dizaines de véhicules, cela peut donner un arrêt complet du trafic.

Mathématiquement, on peut modéliser cela avec une suite :

v_{n+1} = v_n - \delta

où [math]v_n[/math] est la vitesse de la voiture numéro [math]n[/math] dans la file, et [math]\delta[/math] la petite perte de vitesse transmise à chaque fois.

Exemple :

• La 1ʳᵉ voiture ralentit de 2 km/h → [math]v_1 = 98[/math].
• La 2ᵉ voiture ralentit de 2 km/h supplémentaires → [math]v_2 = 96[/math].
• La 3ᵉ descend à 94 km/h…

Au bout de 10 voitures, la perte atteint 20 km/h → [math]v_{10} = 80[/math].

Et si la file est longue, on finit par créer un vrai bouchon alors qu’il n’y avait aucun obstacle au départ.

II. Quand les mathématiques cherchent à optimiser la circulation

1. La courbe fondamentale et les dérivées

On rappelle :

• [math]\rho[/math] = densité (voitures par km, sur une voie).
• [math]v(\rho)[/math] = vitesse moyenne quand la densité vaut [math]\rho[/math].
• [math]q(\rho)=\rho\cdot v(\rho)[/math] = débit (voitures qui passent par heure).

Dans la pratique, plus il y a de voitures, plus la vitesse moyenne baisse. Un modèle simple (et très utilisé pour raisonner) est linéaire :

v(\rho)=v_{\text{max}}\Big(1-\frac{\rho}{\rho_{\text{max}}}\Big),\quad 0\le \rho \le \rho_{\text{max}}.

Alors :

q(\rho)=\rho,v(\rho)=v_{\text{max}}\Big(\rho-\frac{\rho^2}{\rho_{\text{max}}}\Big).

Cette fonction a une forme en cloche. Cherchons son maximum (route à sa capacité optimale).

On dérive :

q'(\rho)=v_{\text{max}}\Big(1-\frac{2\rho}{\rho_{\text{max}}}\Big).

Le point critique vérifie [math]q'(\rho^*)=0 \Rightarrow \rho^*=\frac{\rho_{\text{max}}}{2}[/math].

Et [math]q^{(2)}(\rho)=-\frac{2v_{\text{max}}}{\rho_{\text{max}}}<0[/math] donc c’est bien un maximum.

Sa valeur :

q_{\text{max}}=q(\rho^*)=v_{\text{max}}\cdot\frac{\rho_{\text{max}}}{4}.

Exemple :

Prenons [math]v_{\text{max}}=120\text{ km/h}[/math] et [math]\rho_{\text{max}}=60\text{ veh/km}[/math].

Alors [math]\rho^*=30\text{ veh/km}[/math] et [math]q_{\text{max}}=120\times 60/4=1800\text{ veh/h}[/math].

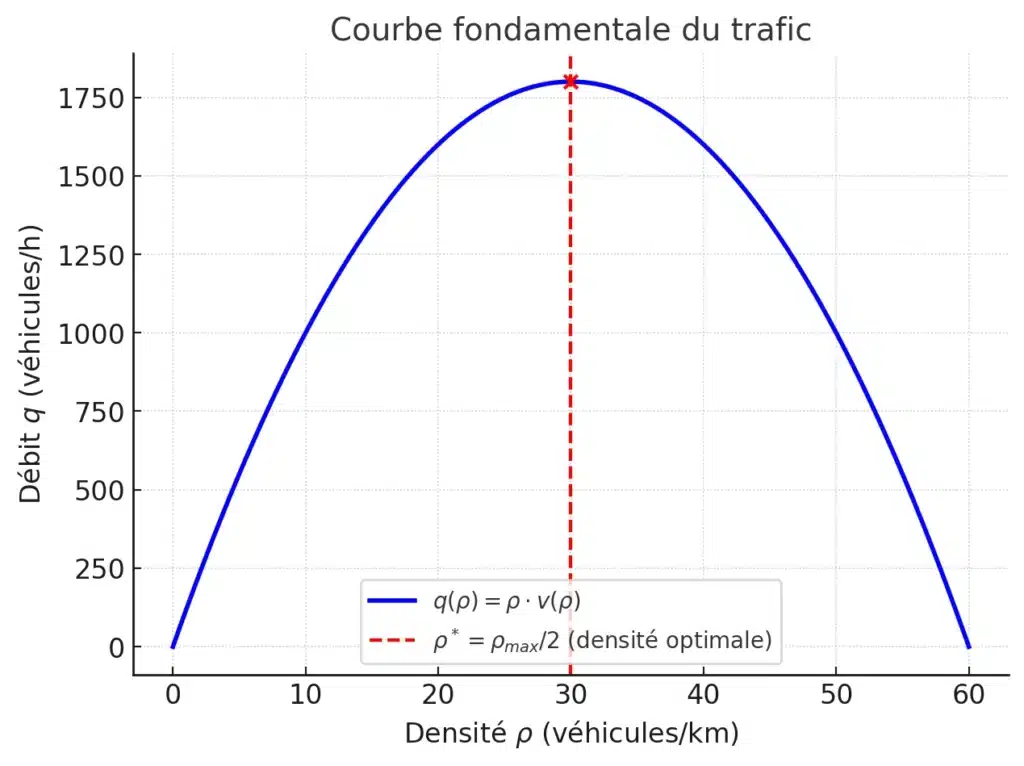
Pour [math]\rho=20\text{ veh/km}[/math] :

q(20)=120\Big(20-\frac{20^2}{60}\Big)=120\Big(20-\frac{400}{60}\Big)\approx 1600 \text{ veh/h} < 1800 \text{ veh/h}.

2. Probabilités et statistiques pour analyser les trajets

Le temps de trajet est une variable aléatoire (accidents, météo, feux, comportements…).

On s’intéresse à :

• La moyenne : [math]E(T)=\mu[/math] (temps « typique »),
• La dispersion : écart-type [math]\sigma[/math] (variabilité d’un jour à l’autre).

Exemple : sur un même parcours, on mesure [math]\mu=30 \text{ min}[/math] et [math]\sigma=15 \text{ min}[/math].

La moyenne seule ne suffit pas : le trajet est très aléatoire (un jour 20 min, un autre 45 min).

Si on modélise (approx.) par une loi normale, on peut estimer des probabilités d’arrivée à l’heure :

• Probabilité d’arriver en moins de 45 min : [math] z=\frac{45-\mu}{\sigma}=\frac{45-30}{15}=1.[/math] Dans la table de la loi normale, [math]P(Z < 1) \approx 0,84[/math]. Donc environ 84% de chances d’arriver avant 45 minutes.
• Probabilité d’être entre 20 et 40 min : [math]z=\frac{20-30}{15}=-0.67 \text{ à } \frac{40-30}{15}=0.67.[/math] La probabilité que [math]Z[/math] soit entre -0,67 et 0,67 est environ 0,50. Donc environ 1 chance sur 2 d’avoir un trajet compris entre 20 et 40 minutes.

Pour réduire [math]\sigma[/math] (trajets plus prévisibles) : lissage de vitesses, feux d’accès aux autoroutes, répartition des itinéraires, et horaires décalés.

III. Les maths pour éviter (ou aggraver) les bouchons

1. Algorithmes et graphes : choisir le meilleur chemin

Pour modéliser un réseau routier, les mathématiques utilisent les graphes :

• Les nœuds représentent les carrefours ou intersections.
• Les arêtes représentent les routes, avec un « poids » qui correspond au temps de trajet.

Chercher le chemin le plus rapide revient alors à trouver le chemin de poids minimal dans ce graphe.

C’est exactement ce que font les GPS (Waze, Google Maps).

Ils utilisent des algorithmes comme Dijkstra pour calculer en quelques millisecondes l’itinéraire optimal entre deux points.

Voici une vidéo à visionner pour pouvoir bien comprendre cet algorithme, et être capable de répondre aux questions du jury :

Exemple :

• Entre la maison et le travail, il existe 3 itinéraires possibles.
• Le GPS évalue pour chacun la distance, la vitesse moyenne, et parfois même la densité de trafic en temps réel.
• Ensuite, il propose celui qui minimise le temps total estimé.

2. Le paradoxe de Braess : quand plus de routes = plus de bouchons

On pourrait croire que construire plus de routes suffit pour réduire les embouteillages… mais c’est faux !

Le paradoxe de Braess montre que parfois, ajouter une nouvelle route aggrave la situation.

Idée intuitive :

• Chaque conducteur cherche à minimiser son temps de trajet personnel.
• Mais si tout le monde raisonne ainsi, le résultat collectif peut être pire qu’avant.

Exemple simple :

• Deux routes parallèles relient A à B. Chacune prend 30 minutes → le trafic est équilibré, 50/50.
• On ajoute une nouvelle petite route rapide entre les deux → chaque conducteur pense pouvoir gagner du temps.
• Résultat : tout le monde prend la même nouvelle combinaison, qui se sature… et le temps de trajet grimpe à 40 minutes pour tout le monde.

Plus de routes = plus de bouchons.

Conclusion

• Les maths décrivent les embouteillages avec des outils simples : densité, débit, propagation des ralentissements.
• Elles optimisent la circulation grâce aux dérivées, probabilités et statistiques.
• Elles aident à la prise de décision via les graphes et algorithmes, tout en révélant des paradoxes comme celui de Braess.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !