Paradoxe de Monty Hall

Introduction

Imagine un jeu télévisé : trois portes, derrière l’une une voiture 🚗, derrière les deux autres… des chèvres 🐐.

Le candidat choisit une porte, disons la porte A. Avant de révéler le résultat, l’animateur Monty Hall, qui sait où est la voiture, ouvre une autre porte (parmi celles non choisies) derrière laquelle il y a une chèvre. Puis il demande au joueur :

Voulez-vous rester sur votre choix initial, ou changer de porte ?

Intuitivement, beaucoup pensent que changer ou non revient au même (50% de chance). Mais en réalité, les mathématiques montrent que changer double les chances de gagner. C’est le fameux paradoxe de Monty Hall.

Avant de commencer, voici une vidéo courte et efficace pour bien comprendre le paradoxe 🙂

I. L’arbre des probabilités

1. Sans changer de porte

Notons :

• [math]V_A[/math] : la voiture est derrière la porte A (celle que le joueur a choisie).
• [math]V_B[/math] : la voiture est derrière la porte B.
• [math]V_C[/math] : la voiture est derrière la porte C.

Au départ, la probabilité est simple :

• [math]P(V_A) = 1/3[/math],
• [math]P(V_B) = 1/3[/math],
• [math]P(V_C) = 1/3[/math].

Ensuite, Monty Hall ouvre une des deux autres portes, notons [math]O_B[/math] = « Monty ouvre la porte B » et [math]O_C[/math] = « Monty ouvre la porte C ».

• Si la voiture est derrière A, Monty peut ouvrir B ou C (probabilité [math]1/2[/math] pour chaque).
• Si la voiture est derrière B, Monty est obligé d’ouvrir C ([math]O_C[/math] avec proba 1).
• Si la voiture est derrière C, Monty est obligé d’ouvrir B ([math]O_B[/math] avec proba 1).

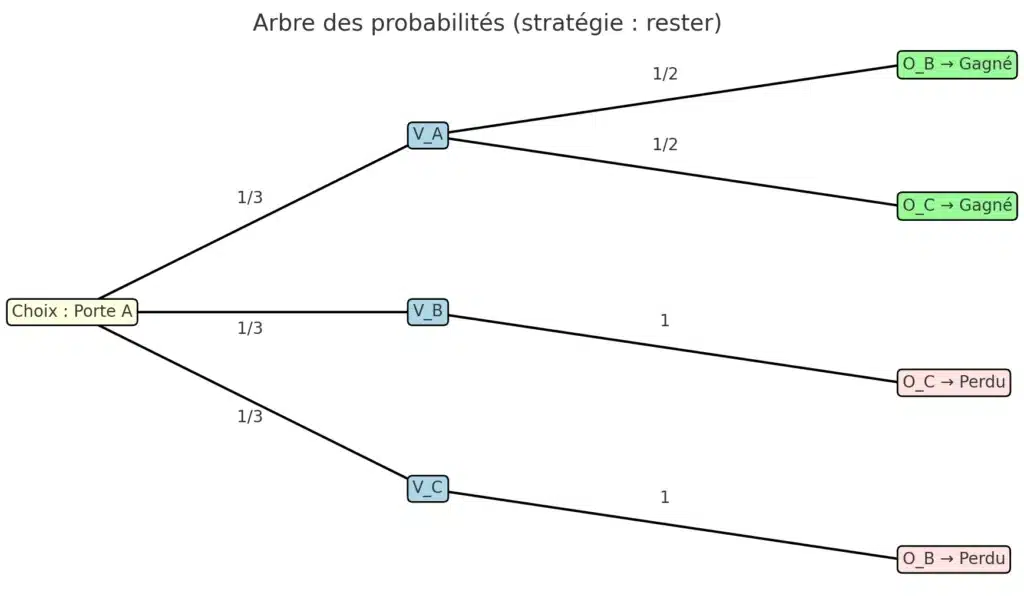
Premier cas : le joueur choisit de rester sur A.

• Si [math]V_A[/math] (probabilité [math]1/3[/math]) → il gagne (la voiture est bien derrière A).
• Si [math]V_B[/math] ou [math]V_C[/math] (probabilité [math]2/3[/math]) → il perd.

2. En changeant de porte

Reprenons le même arbre avec [math]V_A, V_B, V_C, O_B, O_C[/math]. La différence, c’est que maintenant le joueur décide de changer son choix après que Monty a ouvert une porte.

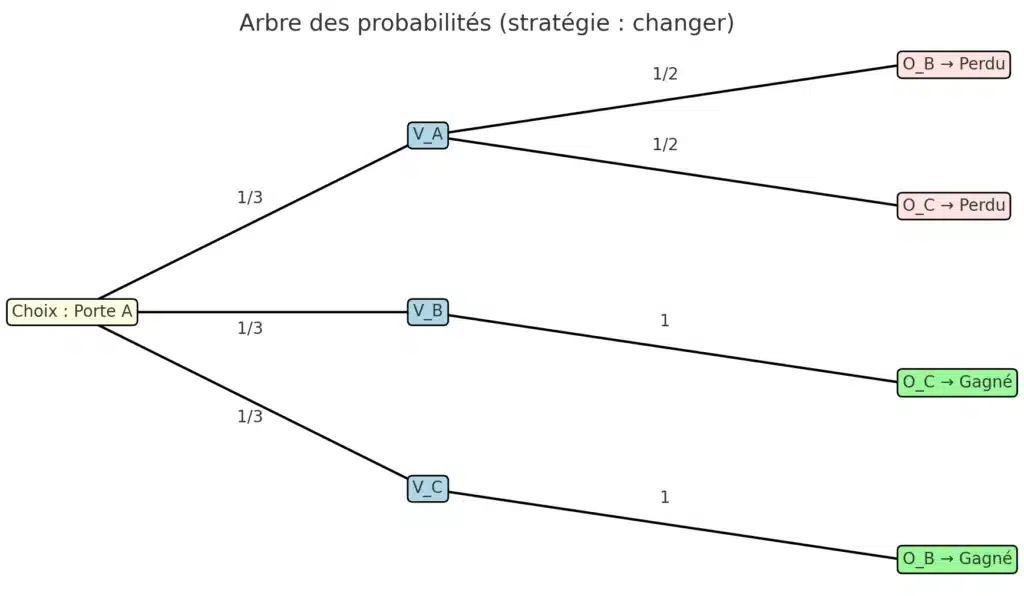
• Si [math]V_A[/math] (probabilité [math]1/3[/math]) → Monty ouvre B ou C → en changeant, le joueur tombe sur l’autre porte, donc une chèvre → il perd.
• Si [math]V_B[/math] (probabilité [math]1/3[/math]) → Monty ouvre C → en changeant vers B, le joueur gagne la voiture.
• Si [math]V_C[/math] (probabilité [math]1/3[/math]) → Monty ouvre B → en changeant vers C, le joueur gagne aussi.

Dans 2 cas sur 3, changer de porte fait gagner.

II. La formule de Bayes et Monty Hall

1. Petit rappel de la formule

La formule de Bayes sert à calculer la probabilité qu’un événement soit vrai en connaissant une information supplémentaire.

Elle s’écrit simplement :

P(A|B) = \frac{P(B|A)\times P(A)}{P(B)}

Pour faire simple : la proba que [math]A[/math] soit vraie sachant [math]B[/math] = (la proba que [math]B[/math] arrive si [math]A[/math] est vraie × la proba que [math]A[/math] soit vraie au départ) ÷ la proba totale que [math]B[/math] arrive.