Une lunette astronomique permet-elle de voir un homme marcher sur la lune ?

Introduction
« Une lunette astronomique permet-elle vraiment de voir un homme marcher sur la Lune ? » La question peut sembler naïve, mais elle cache en réalité des mathématiques très intéressantes. 🌙🔭
Pour y répondre, il faut combiner plusieurs notions du programme : angles en radians, rapports de grandeurs, mais aussi des formules issues de l’optique ondulatoire comme le pouvoir séparateur. Autrement dit, c’est un problème où l’on confronte les ordres de grandeur aux limites physiques des instruments.
I. Taille apparente de l’homme vu depuis la Terre
1. Calcul de l’angle sous-tendu
L’angle sous-tendu (ou angle apparent) d’un objet, c’est l’angle qu’il occupe dans notre champ de vision.
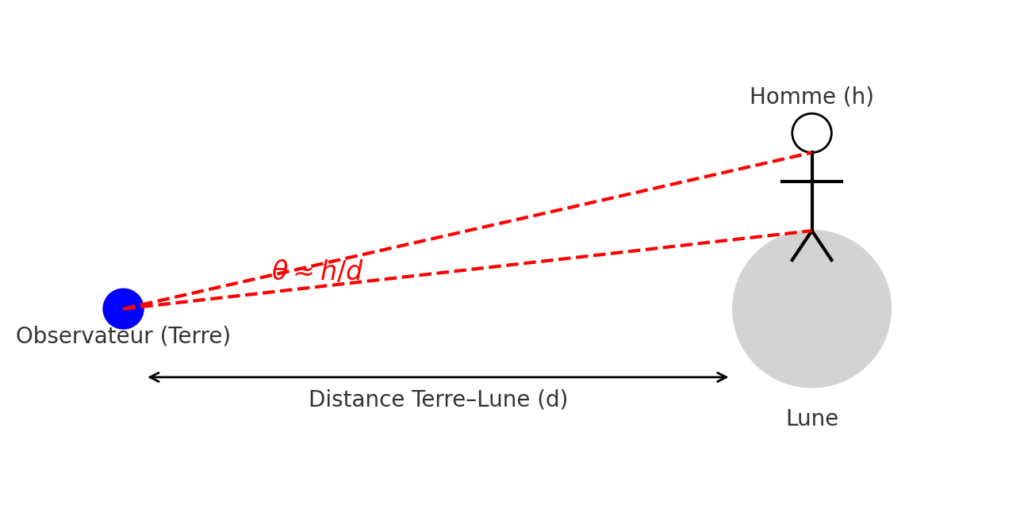
On utilise la formule d’angle sous-tendu (valable pour de petits angles) :
\theta \approx \tfrac{h}{d}.- Taille d’un homme : [math]h \approx 1,8 \text{ m}[/math]
- Distance Terre–Lune : [math]d \approx 3,84 \times 10^8 \text{ m}[/math]
\theta \approx \tfrac{1,8}{3,84 \times 10^8} \approx 4,7 \times 10^{-9} \text{ rad}.Conversion en secondes d’arc (1 rad = 206 265 arcsec) :
\theta \approx 4,7 \times 10^{-9} \times 206,265 \approx 10^{-3} \text{ arcsec}.2. Comparaison avec la taille apparente de la Lune
- Diamètre de la Lune : [math]D = 3,474 \times 10^6 \text{ m}[/math]
- Distance : [math]d = 3,84 \times 10^8 \text{ m}[/math]
\theta_{\text{Lune}} \approx \tfrac{D}{d} = \tfrac{3,474 \times 10^6}{3,84 \times 10^8} \approx 9,0 \times 10^{-3} \text{ rad}En degrés : [math]\theta_{\text{Lune}} \approx 0,52^\circ \approx 1800 \text{ arcsec}[/math]
Comparons :
- Lune : [math]1800 \text{ arcsec}[/math]
- Homme : [math]0,001 \text{ arcsec}[/math]
Rapport :
\tfrac{1800}{0,001} = 1,8 \times 10^6.Un homme sur la Lune apparaît donc 1,8 million de fois plus petit que la Lune vue dans le ciel.
II. Résolution d’une lunette astronomique
1. Pouvoir séparateur (formule de Rayleigh)
Le pouvoir séparateur d’une lunette dépend de la diffraction de la lumière. La formule de Rayleigh donne :
\theta = 1,22 \cdot \tfrac{\lambda}{D}.- Longueur d’onde moyenne de la lumière visible : [math]\lambda \approx 550 \text{ nm} = 5,5 \times 10^{-7} \text{ m}[/math]
- Diamètre d’un objectif amateur : [math]D = 10 \text{ cm} = 0,10 \text{ m}[/math]
\theta = 1,22 \cdot \tfrac{5,5 \times 10^{-7}}{0,10} \approx 6,7 \times 10^{-6} \text{ rad}.Conversion en secondes d’arc :
\theta \approx 6,7 \times 10^{-6} \times 206,265 \approx 1,4 \text{ arcsec}.Or, l’homme sur la Lune correspond à [math]10^{-3} \text{ arcsec}[/math].
🔒 La suite est réservée aux membres Premium
Accédez à l’intégralité des 40 sujets rédigés pour le Grand Oral de Maths.
Je veux le Pack Premium







