En quoi les logarithmes sont utiles dans la vie réelle ?

Introduction

Qu’il s’agisse de mesurer la puissance d’un séisme, le bruit d’un avion, la croissance d’une population ou encore l’efficacité d’un algorithme, les logarithmes sont un outil indispensable. Ils permettent de traduire en langage mathématique des phénomènes qui évoluent de façon exponentielle.

Problématique : en quoi les logarithmes sont-ils utiles dans la vie réelle ?

I. Les logarithmes pour mesurer des phénomènes « exponentiels »

1. Échelle des intensités sonores

Quand on parle de son, on utilise souvent les décibels plutôt que l’intensité brute. En effet, l’oreille humaine ne perçoit pas les sons de façon linéaire : si on multiplie l’intensité par 10, on n’a pas l’impression que le bruit est « 10 fois plus fort ».

Pour traduire cette perception, on utilise une échelle logarithmique :

L = 10 \log_{10}\left(\tfrac{I}{I_0}\right)

où :

• [math]L[/math] est le niveau sonore en décibels,
• [math]I[/math] l’intensité du son,
• [math]I_0[/math] une intensité de référence (seuil d’audition).

Par exemple :

• Une conversation normale correspond à environ 60 dB.
• Un avion au décollage atteint environ 120 dB.

On remarque que le bruit de l’avion paraît beaucoup plus fort, alors que l’intensité réelle est un million de fois plus élevée que celle de la conversation. Sans l’échelle logarithmique, on ne pourrait pas manipuler de tels écarts de grandeur !

2. Magnitude des séismes

Les tremblements de terre sont mesurés avec l’échelle de Richter, qui est elle aussi logarithmique.

La magnitude [math]M[/math] d’un séisme est donnée par :

M = \log_{10}\left(\tfrac{A}{A_0}\right)

où :

• [math]A[/math] est l’amplitude mesurée,
• [math]A_0[/math] une amplitude de référence.

Conséquence directe :

• Quand la magnitude augmente d’une unité, l’amplitude des secousses est multipliée par 10.
• Entre magnitude 6 et magnitude 8, l’amplitude est donc multipliée par [math]10^2 = 100[/math].

Cela explique pourquoi deux séismes qui semblent « proches » dans leur valeur peuvent avoir des conséquences radicalement différentes.

II. Les logarithmes pour résoudre des équations et modéliser des croissances

1. Temps de doublement en économie et en démographie

Beaucoup de phénomènes réels suivent une croissance exponentielle. On peut modéliser une population ou un capital avec :

N(t) = N_0 e^{rt}

où :

• [math]N_0[/math] est la valeur initiale,
• [math]r[/math] est le taux de croissance,
• [math]t[/math] le temps.

Une question pratique est de savoir au bout de combien de temps la population double. On cherche donc [math]T[/math] tel que :

N(T) = 2 N_0.

En remplaçant :

N_0 e^{rT} = 2 N_0 \quad \Rightarrow \quad e^{rT} = 2 \quad \Rightarrow \quad T = \tfrac{\ln 2}{r}.

Exemple concret :

Si une population croît de 2 % par an, alors [math]r=0,02[/math].

On obtient :

T = \tfrac{\ln 2}{0,02} \approx 34,7 \text{ ans}.

Donc la population double en environ 35 ans.

2. Radioactivité et demi-vie

En physique, la décroissance radioactive se modélise par une fonction exponentielle décroissante :

N(t) = N_0 e^{-\lambda t}

où :

• [math]N_0[/math] est la quantité initiale de noyaux,
• [math]\lambda[/math] est la constante radioactive,
• [math]t[/math] le temps.

La demi-vie [math]T_{1/2}[/math] est le temps au bout duquel il ne reste que la moitié de la substance :

N(T_{1/2}) = \tfrac{N_0}{2}.

Donc :

N_0 e^{-\lambda T_{1/2}} = \tfrac{N_0}{2} 
\;\;\Rightarrow\;\; e^{-\lambda T_{1/2}} = \tfrac{1}{2} 
\;\;\Rightarrow\;\; T_{1/2} = \tfrac{\ln 2}{\lambda}.

Application : le carbone 14 a une demi-vie d’environ 5730 ans. C’est grâce à cette propriété que les scientifiques peuvent dater des vestiges archéologiques : en mesurant la proportion de carbone 14 restant dans un os ou un tissu, ils estiment le temps écoulé depuis la mort de l’organisme.

D’ailleurs, c’est le même genre de chose qui est utilisé en criminologie (je vous conseille d’aller checker l’autre sujet de Grand Oral).

III. Les logarithmes dans l’informatique et la science des données

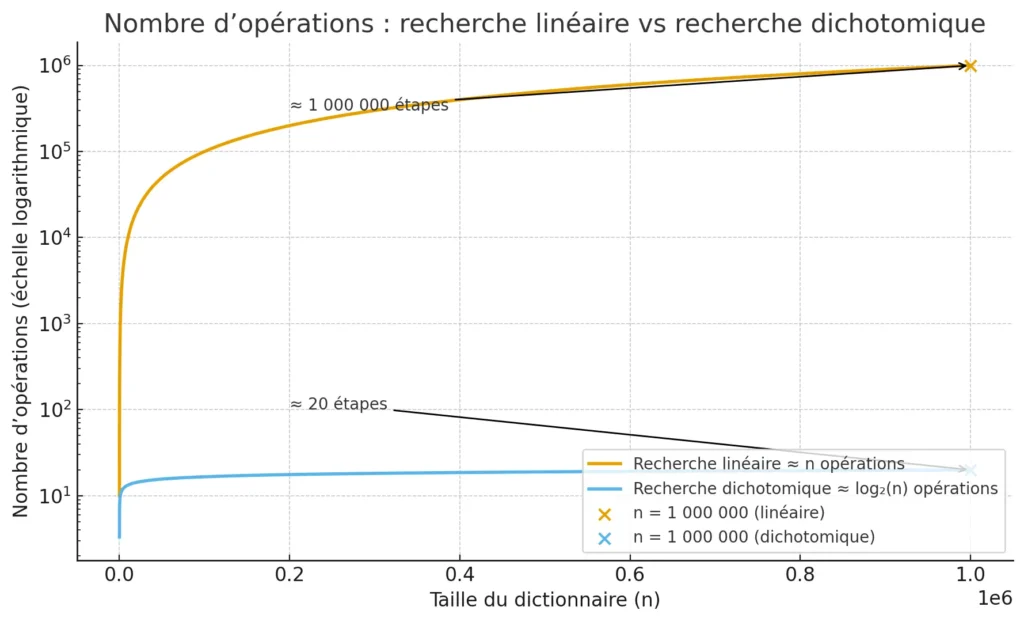
1. Complexité algorithmique

En informatique, on s’intéresse au nombre d’opérations nécessaires pour résoudre un problème.

Un exemple classique est la recherche dichotomique :

• On veut chercher un mot dans un dictionnaire trié.
• À chaque étape, on coupe le dictionnaire en deux et on regarde dans la bonne moitié.
• Au bout de [math]\log_2(n)[/math] étapes environ, on trouve l’élément (ou on prouve qu’il n’existe pas).

Exemple :

Si [math]n = 1000000[/math] (un million de mots), alors :

\log_2(1000000) \approx 20.

Autrement dit, 20 étapes suffisent pour retrouver un mot parmi un million. Sans logarithmes, il faudrait imaginer parcourir tout le dictionnaire, soit un million d’opérations.

2. Information et probabilités

Les logarithmes sont aussi au cœur de la théorie de l’information (Shannon).

L’entropie mesure l’incertitude d’une expérience aléatoire :

H = - \sum p_i \log_2(p_i)

où [math]p_i[/math] est la probabilité de chaque issue.

Exemple simple :

Si on lance une pièce équilibrée ([math]p=0,5[/math] pour pile et face), alors :

H = - (0,5 \log_2(0,5) + 0,5 \log_2(0,5)) = 1.

On dit que le résultat contient 1 bit d’information.

Si la pièce est biaisée (par ex. [math]p=0,9[/math] pour pile), alors :

H \approx 0,47.

Dans ce cas, l’information est moins grande, car l’issue est plus prévisible.

Conclusion

• Les logarithmes permettent de mesurer des phénomènes exponentiels (sons, séismes).
• Ils servent à résoudre des équations liées à la croissance ou à la décroissance (population, radioactivité).
• Ils sont essentiels en informatique et en science des données pour analyser la complexité et l’information.

Pour ce sujet de Grand Oral, l’idée était vraiment de vous lister toutes les choses que vous pouvez aborder, mais je vous conseille fortement de vous concentrer sur une ou deux applications et les développer à fond. Cela vous permettra de vraiment mieux vous approprier le sujet !

Je vous conseille aussi de visionner la vidéo ci-dessous pour le côté historique, cela pourra vous être utile pour la partie échange avec le jury 🙂

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !