Comment déterminer l’heure de décès d’une personne ?

Introduction

La criminologie fascine souvent parce qu’elle mêle enquête, sciences et un peu de mystère. Parmi les questions clés auxquelles doivent répondre les experts : à quelle heure une personne est-elle morte ? Cette estimation est essentielle pour une enquête judiciaire, et étonnamment… les mathématiques jouent un rôle majeur.

En effet, après la mort, le corps humain se refroidit progressivement jusqu’à atteindre la température ambiante. Ce phénomène peut être modélisé par des outils que l’on étudie au lycée : fonctions exponentielles, suites, statistiques.

Problématique : comment les mathématiques, en particulier les fonctions exponentielles et les statistiques, permettent-elles de modéliser le refroidissement d’un corps et d’estimer l’heure de décès ?

I. La température du corps : une décroissance modélisable

1. Refroidissement du corps = décroissance exponentielle

Après la mort, le corps humain cesse de produire de la chaleur et sa température diminue progressivement pour tendre vers celle de son environnement.

Mathématiquement, ce type de phénomène est bien représenté par une décroissance exponentielle :

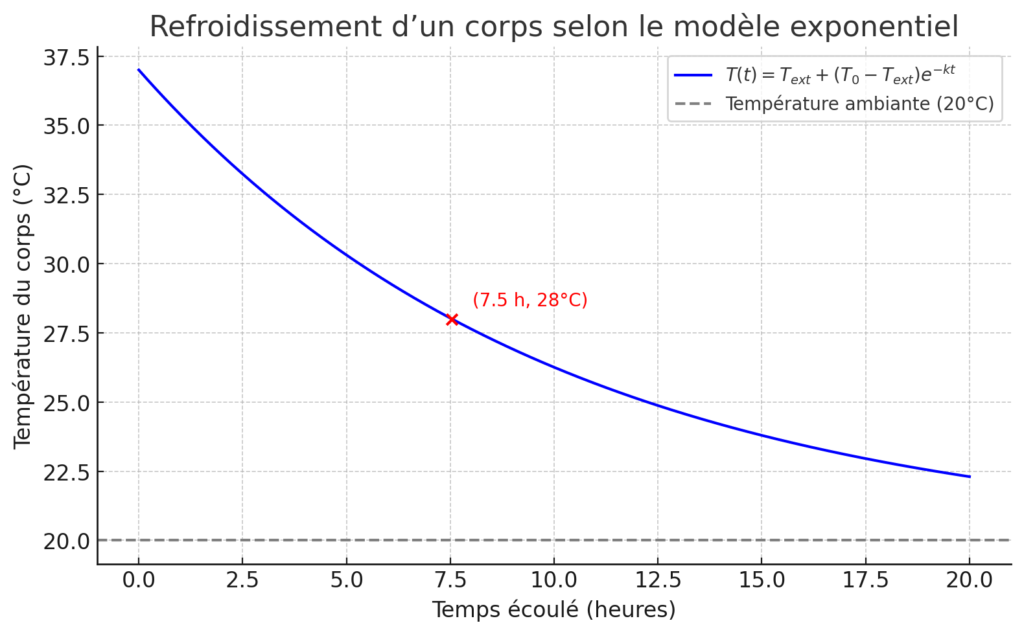
T(t) = T_{\text{ext}} + (T_0 - T_{\text{ext}})\times e^{-kt}.

• [math]T(t)[/math] : température du corps au temps [math]t[/math] (en heures après la mort),
• [math]T_{\text{ext}}[/math] : température ambiante,
• [math]T_0[/math] : température initiale du corps (≈ 37°C),
• [math]k[/math] : constante de refroidissement (dépend de la corpulence, vêtements, environnement).

2. Exemple concret d’application

Imaginons un corps retrouvé dans une pièce à [math]20^\circ C[/math], avec une température mesurée du corps de [math]28^\circ C[/math].

On suppose [math]T_0 = 37^\circ C[/math] et une constante de refroidissement [math]k = 0,1 h^{-1}[/math].

Formule :

T(t) = 20 + (37 - 20)\times e^{-0,1t}.

Donc :

T(t) = 20 + 17 e^{-0,1t}.

On veut trouver [math]t[/math] tel que [math]T(t) = 28[/math].

28 = 20 + 17 e^{-0,1t}

8 = 17 e^{-0,1t}

e^{-0,1t} = \tfrac{8}{17}

-0,1t = \ln\left(\tfrac{8}{17}\right)

t = -\tfrac{1}{0,1}\ln\left(\tfrac{8}{17}\right)

Calcul numérique :

t \approx -10 \times \ln(0,47) \approx 7,5 \text{ heures}.

Cela signifie que la personne est probablement morte environ 7 heures et 30 minutes avant la découverte du corps. Par exemple, si le corps a été trouvé à 7h du matin, le décès aurait eu lieu vers 23h30 la veille.

II. Les statistiques pour réduire l’incertitude

1. Variabilité des mesures

La méthode du refroidissement n’est jamais exacte à la minute près.

En effet, la température d’un corps dépend de plusieurs facteurs :

• les vêtements (un manteau ralentit le refroidissement),
• la corpulence (plus une personne est massive, plus le refroidissement est lent),
• l’environnement (un corps dans une pièce à 25 °C ne se refroidit pas comme à 10 °C).

Résultat : deux personnes mortes à la même heure peuvent présenter des températures légèrement différentes.

C’est pourquoi les experts introduisent un intervalle d’incertitude : par exemple, « décès estimé il y a 13 h ± 1 h ».

2. Outils statistiques simples

Pour quantifier cette incertitude, on peut utiliser la loi normale.

On suppose que le temps de refroidissement suit une distribution centrée autour d’une valeur moyenne [math]\mu[/math], avec une certaine variabilité mesurée par l’écart-type [math]\sigma[/math].

La formule du z-score est :

z = \tfrac{x - \mu}{\sigma}

où :

• [math]x[/math] est la valeur observée,
• [math]\mu[/math] la moyenne estimée,
• [math]\sigma[/math] la dispersion typique.

Exemple concret :

Un modèle indique que la mort est survenue en moyenne à 23 h (soit [math]\mu = 23[/math]), avec un écart-type de [math]\sigma = 1[/math] heure.

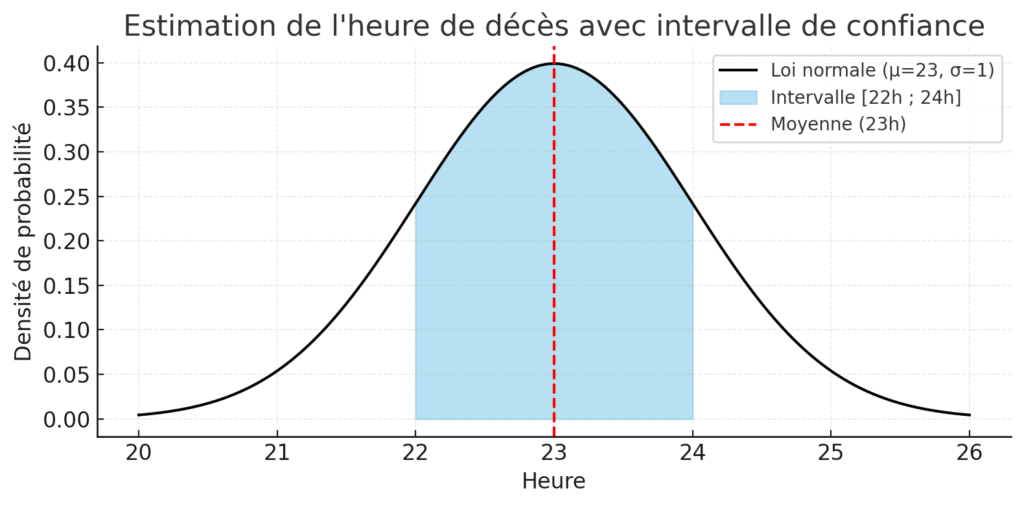
On calcule [math] z_1 = \tfrac{22 – 23}{1} = -1, \quad z_2 = \tfrac{24 – 23}{1} = 1[/math]. Cela correspond à environ 68 % de chances (règle des ±1 écart-type pour la loi normale).

Ainsi, au lieu d’annoncer une seule valeur (« mort à 23 h »), les experts peuvent dire : « avec 68 % de probabilité, le décès a eu lieu entre 22 h et minuit ».

III. Autres méthodes scientifiques avec un modèle mathématique simple

1. Entomologie légale et suites

Lorsqu’un corps reste exposé, il est rapidement colonisé par des insectes (mouches, coléoptères). Les larves grandissent de façon régulière en fonction du temps et de la température ambiante.

Cela peut se modéliser avec une suite arithmétique ou une fonction linéaire simple.

Exemple :

• Une larve mesure 2 mm le premier jour.
• Elle grandit de +2 mm par jour.
• On a donc la suite : [math]u_{n} = 2n[/math], où [math]u_n[/math] est la taille de la larve après [math]n[/math] jours.

Si on mesure une larve de 10 mm, alors :

u_n = 10 \quad \Rightarrow \quad 2n = 10 \quad \Rightarrow \quad n = 5

2. Évolution chimique linéaire

Une autre méthode consiste à mesurer certains composés chimiques qui s’accumulent après la mort.

Exemple classique : le potassium dans l’humeur vitrée de l’œil (liquide oculaire).

On peut modéliser sa concentration par une fonction affine :

C(t) = a \cdot t + b,

où :

• [math]C(t)[/math] est la concentration mesurée,
• [math]t[/math] le temps depuis la mort,
• [math]a[/math] et [math]b[/math] des constantes expérimentales.

Exemple numérique :

• On mesure [math]C = 12[/math].
• On connaît [math]a = 0,2[/math] et [math]b = 3[/math].
  Alors :

12 = 0,2t + 3 \quad \Rightarrow \quad 0,2t = 9 \quad \Rightarrow \quad t = 45 \text{ h}.

Ici, on estime donc que la mort remonte à environ 45 heures.

Conclusion

• La détermination de l’heure du décès découle d’une analyse mathématique fondée sur plusieurs modèles.
• De l’exponentielle (refroidissement du corps) aux lois statistiques (incertitude), en passant par les modèles linéaires(insectes, potassium), les maths apportent des outils concrets aux enquêteurs.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !