Quel est le rôle des mathématiques dans l’architecture ?

Introduction

Quand on observe une cathédrale, un pont ou un gratte-ciel, on voit surtout l’esthétique. Mais derrière chaque ligne et chaque forme, il y a des mathématiques 🙂

L’objectif de ce sujet est de montrer comment, à différents niveaux, les mathématiques guident les architectes : elles permettent de créer l’harmonie des proportions, d’assurer la stabilité des structures et d’innover grâce aux outils modernes.

I. Les mathématiques pour concevoir l’harmonie et les proportions

1. Le nombre d’or et les suites de Fibonacci

Depuis l’Antiquité, les architectes cherchent à construire des bâtiments «harmonieux» aux yeux de l’homme. Les mathématiques apportent une réponse à travers le nombre d’or, noté [math]\varphi[/math].

Il est défini comme la solution positive de l’équation :

\dfrac{a+b}{a} = \dfrac{a}{b}

ce qui conduit à :

\varphi = \dfrac{1+\sqrt{5}}{2} \approx 1{,}618.

Un rectangle dont le rapport longueur/largeur est proche de [math]\varphi[/math] est appelé rectangle d’or. On en retrouve dans l’architecture du Parthénon ou dans les proportions des façades gothiques. Les mathématiques donnent donc un critère objectif pour définir ce qui est perçu comme «esthétique».

Ce nombre est aussi lié aux suites de Fibonacci, définies par :

u_0 = 0, u_1 = 1, u_{n+1} = u_n + u_{n-1}.

La suite commence par [math]0,1,1,2,3,5,8,13,21,34,\dots[/math].

Si l’on considère les rapports [math]\dfrac{u_{n+1}}{u_n}[/math], ils se rapprochent de plus en plus de [math]\varphi[/math].

Exemples numériques :

\dfrac{8}{5} = 1{,}6;\quad \dfrac{13}{8} = 1{,}625;\quad \dfrac{21}{13} \approx 1{,}615.

Cependant, l’harmonie visuelle ne se limite pas au nombre d’or. D’autres éléments mathématiques, comme les symétries, structurent aussi l’esthétique des bâtiments.

2. Symétries et géométrie dans les plans

L’architecture utilise abondamment les symétries, qui sont étudiées en géométrie plane. Elles permettent de créer des motifs répétitifs et équilibrés, visibles dans les mosaïques, les vitraux ou les dômes.

• Symétrie axiale : un point [math]M(x,y)[/math] est envoyé sur [math]M'(x,-y)[/math] si l’axe est l’axe des abscisses.
• Symétrie centrale : si le centre est O, [math]M(x,y)[/math] devient [math]M'(-x,-y)[/math].
• Rotation d’angle [math]\theta[/math] : un point [math]x,y[/math] est transformé en

x',y' = (x\cos\theta - y\sin\theta,; x\sin\theta + y\cos\theta).

Ces formules sont directement utilisées pour modéliser des motifs architecturaux : rosaces des cathédrales (rotations), façades symétriques (symétries axiales), mosaïques arabes (symétries centrales et translations).

Un exemple plus avancé est celui des pavages de Penrose : deux losanges de tailles différentes permettent de couvrir le plan sans répétition périodique, mais avec des symétries locales. Certains architectes contemporains s’en sont inspirés pour créer des décors innovants.

Après avoir vu comment les mathématiques guident l’esthétique et l’harmonie des constructions, intéressons-nous maintenant à un autre rôle essentiel : assurer la solidité des structures grâce à la trigonométrie et aux fonctions.

II. Les mathématiques pour assurer la solidité des structures

1. Trigonométrie et calculs d’angles

Un bâtiment n’est pas seulement fait pour être beau : il doit aussi être stable et solide. Les mathématiques, et en particulier la trigonométrie, sont indispensables pour déterminer les dimensions et les angles corrects.

Prenons un exemple simple : un toit en pente.

On connaît la largeur totale de la maison [math]L[/math] et l’angle d’inclinaison du toit [math]\theta[/math].

On se place dans un triangle rectangle où la moitié de la largeur vaut [math]\tfrac{L}{2}[/math]. On a alors :

\tan(\theta) = \dfrac{h}{L/2}

d’où :

h = \dfrac{L}{2}\tan(\theta)

Exemple numérique :

Si une maison mesure [math]L = 10[/math] m de large et que l’angle du toit est [math]\theta = 30^\circ[/math], alors :

h = \dfrac{10}{2}\times \tan(30^\circ) = 5\times \dfrac{\sqrt{3}}{3} \approx 2{,}89 \text{ m}.

Cette formule simple permet à l’architecte de choisir un angle qui évacue bien la pluie ou la neige tout en restant stable.

2. Optimisation et calculs de charges

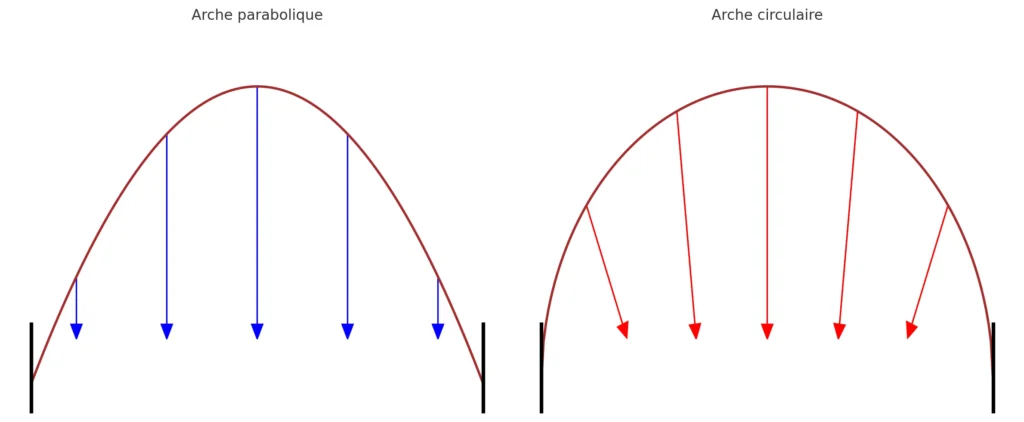
Les architectes de l’Antiquité utilisaient des arcs en demi-cercle, mais les mathématiques ont montré qu’une autre forme est plus résistante : la parabole.

Considérons une arche modélisée par une parabole d’équation :

y = ax^2, \quad a>0.

Cette forme a une propriété remarquable : lorsqu’une charge verticale (comme le poids de la voûte) s’applique, la force est transmise de façon uniforme vers le sol. En d’autres termes, la parabole suit la trajectoire naturelle de la poussée.

À l’inverse, un demi-cercle d’équation :

x^2 + y^2 = R^2

transmet des forces latérales plus importantes, ce qui risque de faire s’écarter les piliers.

On peut même comparer :

• Dans une parabole, la résultante des forces est verticale → elle est absorbée efficacement par les fondations.
• Dans un cercle, la résultante n’est pas verticale → il faut ajouter des contreforts pour compenser (comme dans les cathédrales gothiques).

III. Les mathématiques pour innover et modéliser

1. Modèles géométriques et calculs modernes

Aujourd’hui, l’architecture moderne ne peut pas se passer de la géométrie dans l’espace.

Chaque point d’un bâtiment peut être représenté par des coordonnées [math]x,y,z[/math]. Cela permet de décrire des objets complexes comme :

• un plan, d’équation [math]ax + by + cz + d = 0[/math],
• une sphère, d’équation [math]x^2 + y^2 + z^2 = R^2[/math],
• un cylindre, par exemple [math]x^2 + y^2 = R^2[/math].

Ces équations servent à concevoir des formes célèbres :

• coupoles sphériques (comme au Panthéon de Rome ou dans les stades modernes),
• gratte-ciel cylindriques ou prismatiques,
• structures en verre aux formes complexes (modélisées par des surfaces paramétriques).

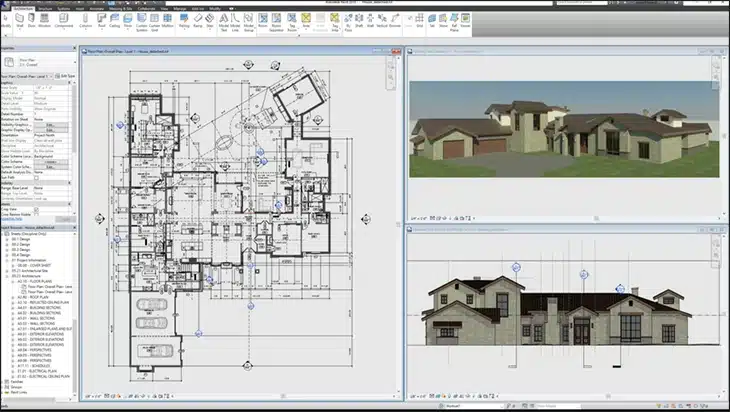
Aujourd’hui, les logiciels de conception assistée par ordinateur (CAO) reposent sur ces mathématiques : chaque élément est défini par des équations géométriques qui permettent de visualiser, modifier et tester virtuellement un bâtiment avant sa construction.

2. Probabilités et statistiques en architecture moderne

Un architecte doit aussi estimer la manière dont un bâtiment sera utilisé afin d’assurer confort et sécurité. Pour cela, il utilise des outils statistiques et probabilistes.

• Statistiques descriptives : elles servent à estimer la fréquentation moyenne d’un lieu.
  Exemple : si un centre commercial reçoit en moyenne [math]5000[/math] visiteurs par jour, avec un pic de [math]8000[/math] le week-end, il faut dimensionner les escaliers et sorties pour ces valeurs maximales.
• Probabilités : elles permettent de calculer les risques d’événements rares mais importants (incendie, séisme).
  Exemple : si la probabilité annuelle d’un séisme fort est [math]p=0{,}01[/math], alors la probabilité qu’il survienne au moins une fois en 30 ans est :

\mathbb{P}(\text{au moins un séisme}) = 1 - (1-p)^{30} = 1 - 0{,}99^{30} \approx 0{,}26.

Cela signifie qu’il y a environ 26 % de chances d’avoir un séisme sur cette période → les normes de construction doivent en tenir compte.

Un autre exemple est le dimensionnement d’un stade. Si on estime grâce aux données que le nombre de spectateurs suit une loi normale de moyenne [math]\mu=30,000[/math] et d’écart-type [math]\sigma=5,000[/math], on peut calculer qu’il faut prévoir au moins [math]\mu + 2\sigma \approx 40,000[/math] places pour couvrir 95 % des situations.

Conclusion

L’architecture est un mélange d’art et de science, et les mathématiques en sont la base cachée. Elles permettent de construire des bâtiments beaux, stables et adaptés à notre époque. Sans maths, l’architecture moderne n’existerait donc tout simplement pas…

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !