Le Dobble

Introduction

Vous connaissez sûrement le jeu Dobble : on retourne deux cartes et, à chaque fois, il y a toujours un symbole en commun. On pourrait croire que c’est juste un hasard bien conçu, mais en réalité, il y a des mathématiques très précises derrière. C’est ce que je vais vous montrer 🙂

I. Mini-Dobble à 7 cartes : incidence et vérifications concrètes (ordre 2)

L’idée est de commencer par un exemple réduit de Dobble : 7 cartes avec 7 symboles seulement. Cela permet de visualiser et de prouver les propriétés sans se perdre dans la complexité du vrai jeu.

1. Mise en place : la matrice d’incidence

On considère 7 cartes et 7 symboles, que l’on note [math]A, B, \dots, G[/math].

Pour représenter la répartition des symboles sur les cartes, on utilise une matrice d’incidence [math]M\in{0,1}^{7\times 7}[/math] :

• chaque ligne correspond à un symbole,
• chaque colonne correspond à une carte,
• [math]M_{i,j}=1[/math] si le symbole [math]i[/math] est présent sur la carte [math]j[/math], et [math]0[/math] sinon.

Dans ce mini-Dobble, chaque carte contient exactement 3 symboles, et chaque symbole apparaît exactement sur 3 cartes.

On a donc les propriétés :

\sum_i M_{i,j}=3 \quad \text{(3 symboles par carte)},

\sum_j M_{i,j}=3 \quad \text{(3 cartes par symbole)}

La règle du Dobble s’écrit joliment avec le produit scalaire :
si l’on prend deux colonnes [math]c\neq c'[/math], leur produit scalaire vaut toujours 1 :

\langle M_{\bullet c},M_{\bullet c'}\rangle = 1.

Autrement dit, deux cartes distinctes ont exactement un symbole en commun.

2. Lecture géométrique : le plan projectif d’ordre 2 (plan de Fano)

Ce mini-Dobble correspond exactement au plan de Fano, qui est le plus petit exemple de plan projectif (d’ordre 2).

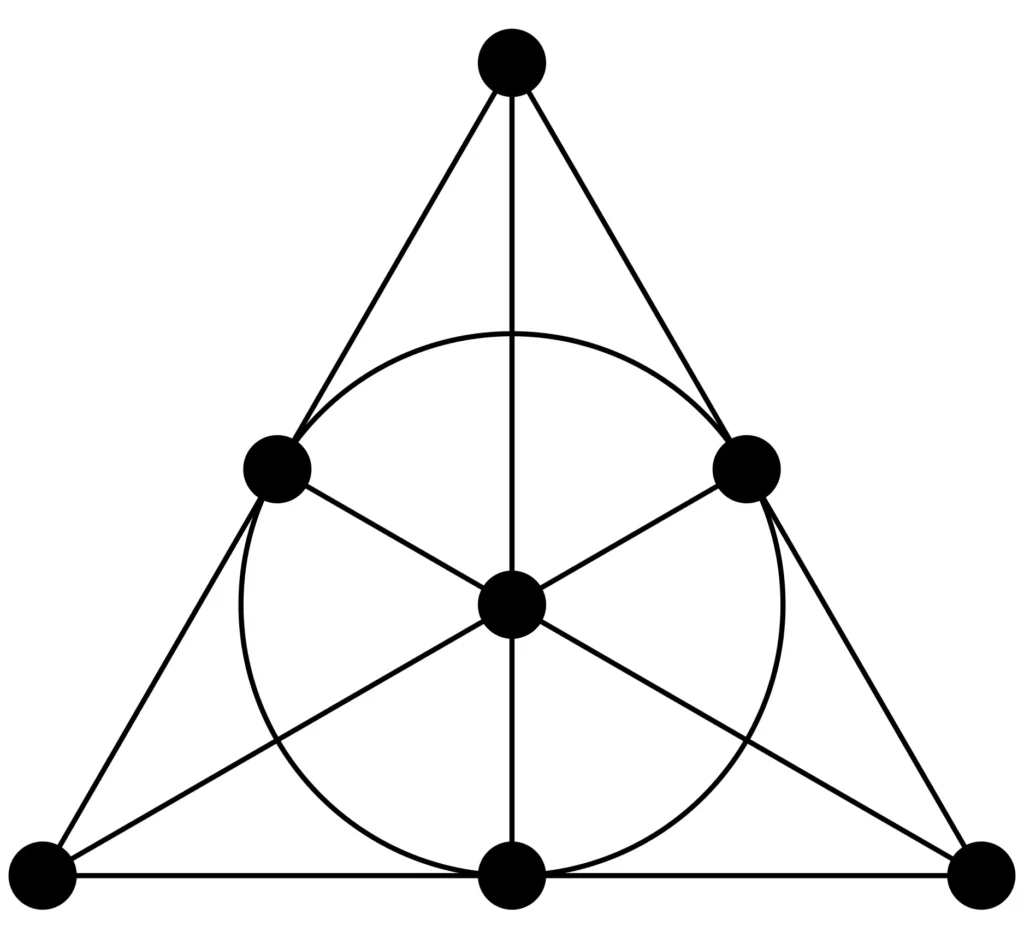
Un plan projectif repose sur trois axiomes fondamentaux :

1. Toute paire de lignes se coupe en un point unique.
2. Par toute paire de points passe exactement une ligne.
3. Il existe 4 points tels que pas plus de deux d’entre eux ne soient alignés (condition de non-dégénérescence).

On peut faire la correspondance suivante :

• Point = symbole ;
• Ligne = carte.

On obtient alors la structure suivante :

• 7 points, 7 lignes,
• 3 points sur chaque ligne,
• 3 lignes passant par chaque point.

Cela correspond exactement aux propriétés du mini-Dobble.

Une conséquence intéressante : si l’on choisit 3 points (donc 3 symboles) qui n’appartiennent pas à une même ligne, alors il n’existe aucune carte qui les regroupe.

Au passage, n’hésitez pas à aller regarder la vidéo ci-dessous qui illustre bien ce sujet sous forme vidéo :

II. Théorie générale : du mini-Dobble aux plans projectifs d’ordre [math]n[/math]

L’exemple du mini-Dobble à 7 cartes correspond au plan projectif d’ordre 2. On peut maintenant généraliser cette idée à un plan projectif d’ordre [math]n[/math].

1. Axiomes et paramètres

Un plan projectif d’ordre [math]n[/math] est une structure combinatoire qui respecte les axiomes :

1. Toute paire de lignes se coupe en un point unique.
2. Par toute paire de points passe une unique ligne.
3. La structure n’est pas dégénérée (il existe au moins 4 points dont pas plus de deux ne sont alignés).

De ces axiomes découlent les paramètres suivants :

• Nombre total de points (et de lignes) :
  [math]v = n^2+n+1[/math].
• Nombre de points par ligne (et de lignes par point) :
  [math]k = r = n+1[/math].
• Toute paire de points est sur une unique ligne :
  [math]\lambda = 1[/math].

2. Vue matricielle

On peut traduire tout cela dans une matrice d’incidence [math]M \in {0,1}^{v \times v}[/math], où les lignes représentent les points et les colonnes représentent les lignes (ou cartes, dans le langage Dobble).

Propriétés :

• Somme de chaque ligne et de chaque colonne :
  [math]\sum_i M_{i,j} = k = n+1.[/math]
• Produit scalaire de deux colonnes :
  • même colonne : [math]\langle c,c\rangle = k[/math] (car il y a [math]k[/math] symboles par carte),
  • colonnes distinctes : [math]\langle c,c’\rangle = \lambda = 1[/math] (car deux cartes ont toujours un symbole commun).

En langage matriciel, on obtient :

M^\top M = (k-1)I + J,

où [math]I[/math] est la matrice identité et [math]J[/math] est la matrice pleine de 1.

Ces relations expriment précisément les règles du jeu :

• [math]\langle c,c\rangle = k[/math] signifie qu’une carte contient [math]k=n+1[/math] symboles.
• [math]\langle c,c’\rangle=1[/math] (si [math]c\neq c'[/math]) signifie que deux cartes ont exactement un symbole en commun.

Ainsi, le Dobble n’est rien d’autre qu’un exemple concret de plan projectif.

III. Le Dobble «réel» : ordre 7, deck commercial à 55 cartes

1. Ce que dicte la théorie (ordre 7)

Dans le vrai jeu Dobble, chaque carte contient 8 symboles.

Or, dans un plan projectif :

• si [math]k=n+1=8[/math], alors l’ordre est [math]n=7[/math].
• On obtient donc un plan projectif d’ordre 7, qui devrait contenir :

[math]v=n^2+n+1 = 7^2+7+1=57[/math] points et lignes, c’est-à-dire 57 symboles et 57 cartes.

Les paramètres sont alors :

• [math]k=r=n+1=8[/math], donc 8 symboles par carte et 8 cartes par symbole,
• [math]\lambda=1[/math], ce qui garantit que toute paire de cartes a exactement un symbole commun.

Dans la matrice d’incidence [math]57\times 57[/math], on doit donc avoir au total :

[math]v\cdot k=57\cdot 8 = 456[/math] «1» (chacun correspondant à la présence d’un symbole sur une carte).

C’est le «Dobble parfait» théorique.

2. Le deck vendu : seulement 55 cartes

En pratique, la boîte de Dobble ne contient que 55 cartes.

Il manque donc 2 cartes sur les 57 théoriques.

Conséquence :

• Avec 55 cartes, on observe [math]55\times 8=440[/math] symboles placés,
• alors qu’un plan complet en aurait [math]456[/math].
• Il manque donc 16 occurrences de symboles.

Pour comprendre, faisons un comptage des fréquences des symboles dans le jeu :

• Dans un deck complet, chaque symbole apparaît 8 fois.
• Avec 2 cartes manquantes :
  • Un symbole apparaît 6 fois au lieu de 8 → c’est le symbole commun aux deux cartes absentes.
  • 14 symboles apparaissent 7 fois → ils sont présents sur une seule des deux cartes manquantes.
  • Les 42 autres apparaissent encore 8 fois et ne sont donc pas concernés.

3. Reconstruction des 2 cartes manquantes

La beauté de la structure est que l’on peut reconstruire les deux cartes manquantes uniquement grâce au comptage.

Étape 1 : repérer le symbole commun.

Le symbole qui n’apparaît que 6 fois est nécessairement présent sur les deux cartes manquantes. Appelons-le [math]S[/math]. En pratique, il s’agit du zèbre 🙂

Étape 2 : identifier les symboles candidats.

Les 14 symboles qui apparaissent 7 fois doivent être répartis :

• 7 d’entre eux iront avec [math]S[/math] sur la première carte,
• les 7 autres iront avec [math]S[/math] sur la deuxième carte.

Étape 3 : appliquer la règle d’unicité.

Dans un plan projectif, chaque paire de symboles doit apparaître exactement une fois.

Donc deux symboles qui sont déjà ensemble sur une carte observée ne peuvent pas se retrouver ensemble sur l’une des deux cartes manquantes.

En vérifiant à chaque fois que les paires créées ne violent pas la règle d’unicité, on reconstitue parfaitement les deux cartes manquantes.

Conclusion

Le Dobble paraît être un simple jeu de cartes, mais en réalité il cache une vraie structure mathématique, et c’est grâce à elle qu’il fonctionne si parfaitement.

On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !