Paradoxe de Monty Hall

Introduction
Imagine un jeu télévisé : trois portes, derrière l’une une voiture 🚗, derrière les deux autres… des chèvres 🐐.
Le candidat choisit une porte, disons la porte A. Avant de révéler le résultat, l’animateur Monty Hall, qui sait où est la voiture, ouvre une autre porte (parmi celles non choisies) derrière laquelle il y a une chèvre. Puis il demande au joueur :
Voulez-vous rester sur votre choix initial, ou changer de porte ?
Intuitivement, beaucoup pensent que changer ou non revient au même (50% de chance). Mais en réalité, les mathématiques montrent que changer double les chances de gagner. C’est le fameux paradoxe de Monty Hall.
Avant de commencer, voici une vidéo courte et efficace pour bien comprendre le paradoxe 🙂
I. L’arbre des probabilités
1. Sans changer de porte
Notons :
- [math]V_A[/math] : la voiture est derrière la porte A (celle que le joueur a choisie).
- [math]V_B[/math] : la voiture est derrière la porte B.
- [math]V_C[/math] : la voiture est derrière la porte C.
Au départ, la probabilité est simple :
- [math]P(V_A) = 1/3[/math],
- [math]P(V_B) = 1/3[/math],
- [math]P(V_C) = 1/3[/math].
Ensuite, Monty Hall ouvre une des deux autres portes, notons [math]O_B[/math] = « Monty ouvre la porte B » et [math]O_C[/math] = « Monty ouvre la porte C ».
- Si la voiture est derrière A, Monty peut ouvrir B ou C (probabilité [math]1/2[/math] pour chaque).
- Si la voiture est derrière B, Monty est obligé d’ouvrir C ([math]O_C[/math] avec proba 1).
- Si la voiture est derrière C, Monty est obligé d’ouvrir B ([math]O_B[/math] avec proba 1).
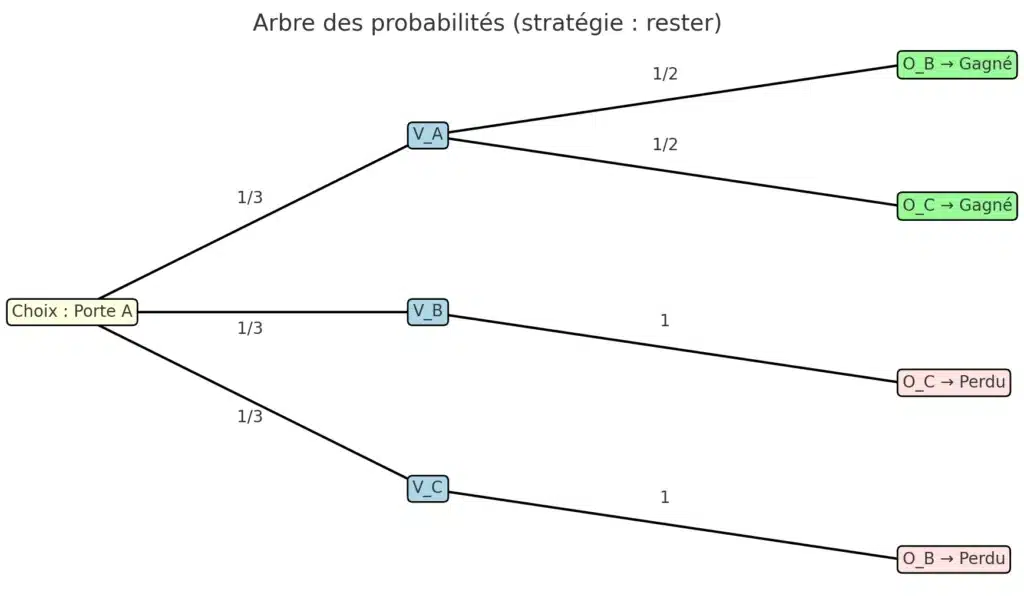
Premier cas : le joueur choisit de rester sur A.
- Si [math]V_A[/math] (probabilité [math]1/3[/math]) → il gagne (la voiture est bien derrière A).
- Si [math]V_B[/math] ou [math]V_C[/math] (probabilité [math]2/3[/math]) → il perd.
2. En changeant de porte
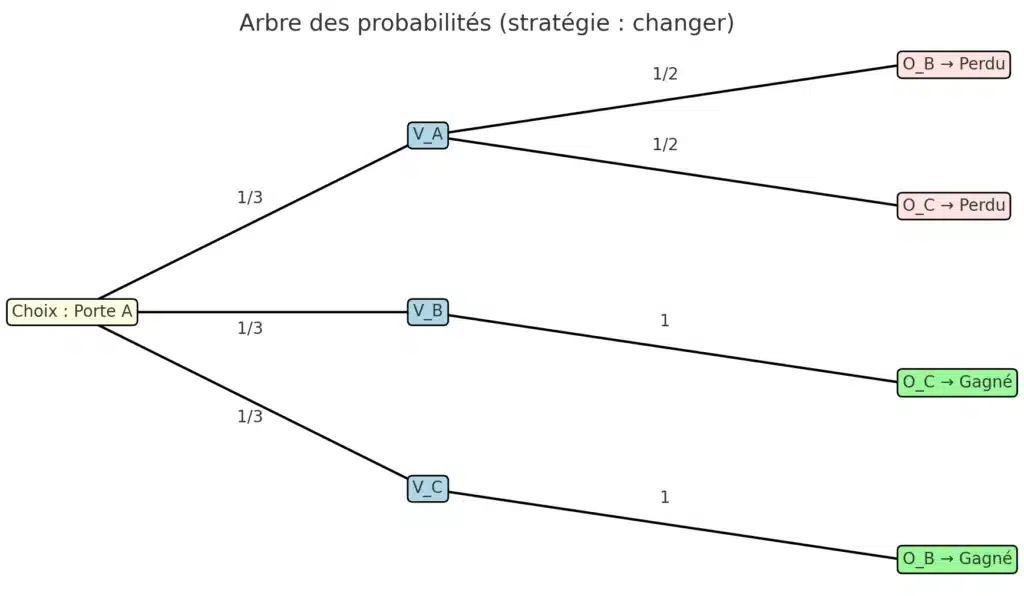
Reprenons le même arbre avec [math]V_A, V_B, V_C, O_B, O_C[/math]. La différence, c’est que maintenant le joueur décide de changer son choix après que Monty a ouvert une porte.
- Si [math]V_A[/math] (probabilité [math]1/3[/math]) → Monty ouvre B ou C → en changeant, le joueur tombe sur l’autre porte, donc une chèvre → il perd.
- Si [math]V_B[/math] (probabilité [math]1/3[/math]) → Monty ouvre C → en changeant vers B, le joueur gagne la voiture.
- Si [math]V_C[/math] (probabilité [math]1/3[/math]) → Monty ouvre B → en changeant vers C, le joueur gagne aussi.
Dans 2 cas sur 3, changer de porte fait gagner.
II. La formule de Bayes et Monty Hall
1. Petit rappel de la formule
La formule de Bayes sert à calculer la probabilité qu’un événement soit vrai en connaissant une information supplémentaire.
Elle s’écrit simplement :
P(A|B) = \frac{P(B|A)\times P(A)}{P(B)}Pour faire simple : la proba que [math]A[/math] soit vraie sachant [math]B[/math] = (la proba que [math]B[/math] arrive si [math]A[/math] est vraie × la proba que [math]A[/math] soit vraie au départ) ÷ la proba totale que [math]B[/math] arrive.
2. Application à Monty Hall
On suppose toujours que le joueur a choisi la porte A au départ.
Cas 1 : Monty ouvre la porte B et on décide de changer de porte
Ici, gagner signifie que la voiture est derrière la porte C.
On veut donc calculer :
P(\text{voiture derrière C | Monty ouvre B})Avec Bayes :
P(V_C | O_B) = \frac{P(O_B|V_C)\times P(V_C)}{P(O_B)}- [math]P(O_B|V_C)=1[/math] car si la voiture est derrière C, Monty est obligé d’ouvrir B.
- [math]P(V_C)=1/3[/math] car chaque porte a la même chance au départ.
- [math]P(O_B)=P(O_B|V_A)\times P(V_A)+P(O_B|V_C)\times P(V_C) = (1/2)\times(1/3) + 1\times(1/3) = 1/2.[/math]
Donc :
P(V_C | O_B) = \frac{1\times(1/3)}{1/2} = 2/3.Cas 2 : Monty ouvre la porte B et on reste sur la porte A
Ici, gagner signifie que la voiture est derrière la porte A.
On veut donc calculer :
P(\text{voiture derrière A | Monty ouvre B})Avec Bayes :
P(V_A | O_B) = \frac{P(O_B | V_A)\times P(V_A)}{P(O_B)}- [math]P(O_B|V_A)=1/2[/math] car si la voiture est derrière A, Monty pouvait ouvrir B ou C avec la même probabilité.
- [math]P(V_A)=1/3[/math] car au départ chaque porte est également probable.
- [math]P(O_B)=1/2[/math] comme déjà calculé dans le cas précédent.
Donc :
P(V_A | O_B) = \frac{(1/2)\times(1/3)}{1/2} = 1/3.On remarque que si Monty ouvre la porte C au lieu de B, le raisonnement est strictement symétrique :
- rester sur A donne [math]1/3[/math],
- changer vers l’autre porte donne [math]2/3[/math].
On retrouve donc exactement les mêmes résultats qu’avec l’arbre de probabilités :
- changer → [math]2/3[/math]
- rester → [math]1/3[/math]
III. Vérifier le paradoxe par un algorithme
1. Algorithme en langage naturel (pseudo-code)
Objectif : comparer la stratégie rester et la stratégie changer.
Initialiser V_gagne_en_changeant = 0
Initialiser V_gagne_sans_changer = 0
Répéter N fois (ex. N = 1000 ou 100000) :
- choix = porte choisie au hasard parmi {A, B, C}
- voiture = position de la voiture au hasard parmi {A, B, C}
- Monty ouvre une porte différente de 'choix' et qui NE contient PAS la voiture
(s'il a le choix entre deux portes chèvres, il en ouvre une au hasard)
- Stratégie "rester" :
si choix == voiture :
V_gagne_sans_changer += 1
- Stratégie "changer" :
switch = l'autre porte (non ouverte par Monty et différente de 'choix')
si switch == voiture :
V_gagne_en_changeant += 1
À la fin :
p_sans_changer = V_gagne_sans_changer / N
p_en_changeant = V_gagne_en_changeant / N
Afficher p_sans_changer et p_en_changeant
Attendu théorique :
- rester ≈ 1/3
- changer ≈ 2/3
2. Exemple concret en Python (résultats réels)
import random
def simulate_monty_hall(n_trials=200000, seed=42):
random.seed(seed)
wins_stay = 0
wins_switch = 0
for _ in range(n_trials):
doors = [0, 1, 2] # 0:A, 1:B, 2:C
car = random.choice(doors) # position de la voiture
choice = random.choice(doors) # choix initial du joueur
# Monty ouvre une porte chèvre différente du choix et de la voiture
possible_opens = [d for d in doors if d != choice and d != car]
opened = random.choice(possible_opens)
# Stratégie rester
if choice == car:
wins_stay += 1
# Stratégie changer : prendre l'autre porte (ni 'choice' ni 'opened')
switch_choice = [d for d in doors if d not in (choice, opened)][0]
if switch_choice == car:
wins_switch += 1
return {
"trials": n_trials,
"wins_stay": wins_stay,
"wins_switch": wins_switch,
"p_stay": wins_stay / n_trials,
"p_switch": wins_switch / n_trials
}
res = simulate_monty_hall()
print(res)
Sortie obtenue (simulation faite) :
- essais : 200 000
- victoires en restant : 66 584 → p ≈ 0,3329
- victoires en changeant : 133 416 → p ≈ 0,6671
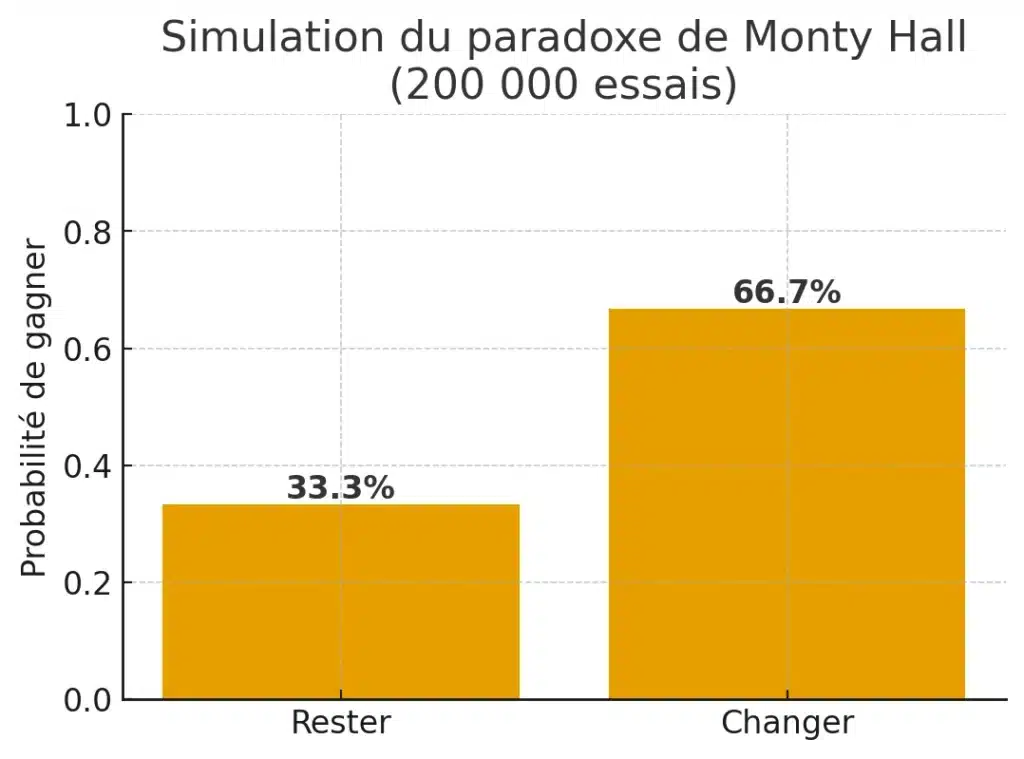
La simulation confirme parfaitement la théorie : rester ≈ 1/3, changer ≈ 2/3.
Conclusion
- Arbre de probabilités : rester → [math]\tfrac{1}{3}[/math], changer → [math]\tfrac{2}{3}[/math].
- Formule de Bayes : on retrouve les mêmes résultats (2/3 en changeant, 1/3 en restant).
- Simulation Python : après 200 000 essais → environ 33% en restant, 67% en changeant.
Les trois approches mènent au même verdict : il vaut toujours mieux changer de porte. 🚪🎉
😏 Fait amusant : même de grands mathématiciens et statisticiens se sont longtemps trompés sur ce paradoxe… preuve que parfois, notre intuition est le pire ennemi des probabilités !
On espère que ce sujet vous aidera, et que vous saurez l’exploiter au mieux pour briller à votre épreuve !








