Comment les mathématiques peuvent aider dans le traitement des cancers ?

Introduction

A. Définition du cancer et de son importance en santé publique

Bienvenue à tous pour ce grand oral sur un sujet crucial : « Le rôle des mathématiques dans le traitement des cancers ». Avant de plonger dans les détails, laissez-moi vous expliquer ce qu’est le cancer. Si l’on consulte un dictionnaire, on peut y lire que c’est une «maladie provoquée par la transformation de cellules qui deviennent anormales et prolifèrent de façon excessive».

Imaginez votre corps comme une ville, avec ses cellules qui jouent des rôles spécifiques, comme les habitants de cette ville. Maintenant, le cancer survient lorsqu’un groupe de cellules « délinquantes » commence à se multiplier de manière incontrôlée, perturbant ainsi l’ordre de la ville et mettant en péril la sécurité de l’ensemble de la ville. Vous comprenez maintenant pourquoi le cancer est une préoccupation majeure en santé publique ! (Notre sujet est de grand oral est donc plutôt pertinent.. hehe)

B. Importance de la recherche de solutions efficaces

Face à cette menace grave, la recherche de solutions efficaces est vitale. Chaque avancée dans le domaine du traitement du cancer peut potentiellement sauver des vies et améliorer la qualité de vie des patients.

C’est pourquoi les efforts des chercheurs et des professionnels de la santé sont continuellement dirigés vers la découverte de nouvelles méthodes de traitement et de prévention.

C. Annonce du sujet : le rôle des mathématiques dans le traitement des cancers

Maintenant, passons à notre sujet du jour : le rôle surprenant des mathématiques dans la lutte contre le cancer.

Eh bien, vous seriez surpris de découvrir comment les équations et les modèles mathématiques peuvent nous aider à mieux comprendre cette maladie et à développer des traitements plus efficaces.

I. Modélisation mathématique des tumeurs cancéreuses

A. Modèles de croissance tumorale

1. Modèle de croissance exponentielle

Le modèle de croissance exponentielle est une représentation mathématique de la croissance rapide et non contrôlée des cellules tumorales. Il suppose une augmentation constante du nombre de cellules avec le temps. Cette croissance exponentielle est souvent observée dans les stades initiaux du cancer, lorsque les cellules cancéreuses se multiplient rapidement sans rencontrer de limitations.

En gros, retenez que dans ce cas, le nombre de cellules cancéreuses ne fait qu’augmenter, et de manière de plus en plus significative. Cependant, ce modèle présente pas mal de limites, c’est pourquoi il n’est pas toujours pertinent.

2. Modèle de croissance logistique

Le modèle de croissance logistique prend en compte les limitations environnementales et physiologiques qui influent sur la croissance tumorale. Contrairement au modèle exponentiel, ce modèle reconnaît que la croissance ne peut pas être infinie en raison de facteurs tels que la disponibilité des nutriments, de l’oxygène et de l’espace. Ainsi, la croissance tumorale atteint éventuellement un plateau, où la multiplication des cellules est compensée par leur mort.

Parlons à présent plus spécifiquement d’un modèle mathématique qui est très souvent utilisé dans le milieu médical : le modèle de Gompertz (ça vous dit quelque chose❓).

L’équation de cette modélisation est :

N(t) = A \cdot e^{B \cdot e^{C \cdot t}}

Où :

A = 10^{12}, B = \ln(10^{-12}),C = -0.09 

Cette équation permet de modéliser la croissance tumorale en fonction du temps (t), en utilisant les paramètres A, B, et C.

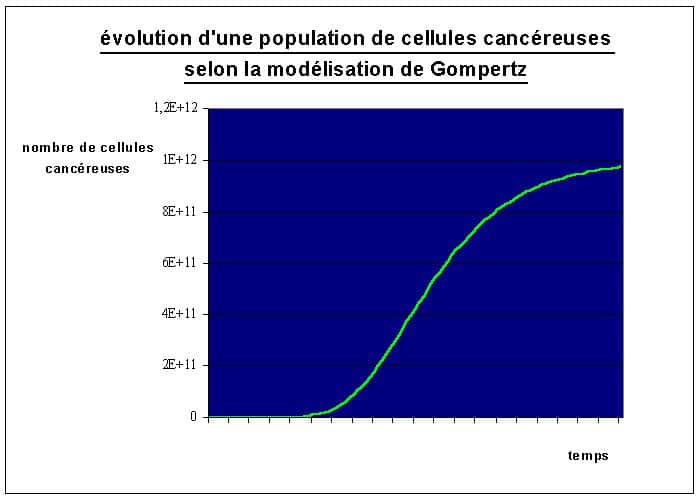
Sur ce graphique, l’axe des abscisses est gradué de manière arbitraire de 0 à 40, car il est difficile d’utiliser une échelle de temps précise. En effet, la vitesse de croissance des différents cancers peut varier considérablement. Certains cancers peuvent se développer rapidement, en seulement 5 ans, tandis que d’autres peuvent prendre jusqu’à 15 ans pour doubler leur taille. Cette variabilité est illustrée par les différentes vitesses de croissance observées.

Observons maintenant la forme de la courbe. Au début, la croissance tumorale est très lente, presque imperceptible, car la courbe reste très proche de l’axe des abscisses. Cette phase initiale correspond à une période où les cellules cancéreuses sont encore peu nombreuses et leur multiplication est limitée.

Ensuite, la croissance commence à s’accélérer progressivement. Cela est dû au fait que les cellules cancéreuses acquièrent des capacités de multiplication plus rapides. Elles deviennent de plus en plus efficaces pour se reproduire, ce qui se traduit par une augmentation significative de la croissance tumorale.

Finalement, la croissance ralentit. Ce ralentissement est causé par une augmentation des pertes cellulaires. À ce stade, les pertes de cellules deviennent équivalentes au nombre de nouvelles cellules créées. Ces pertes sont principalement dues au fait que les cellules cancéreuses perdent leur capacité à réparer leur propre génome. Cette perte de stabilité génétique rend les cellules cancéreuses plus vulnérables aux mutations. Si ces mutations affectent des gènes essentiels à la survie cellulaire, la cellule meurt, entraînant ainsi une diminution du nombre total de cellules.

Pour aller plus loin : ici.

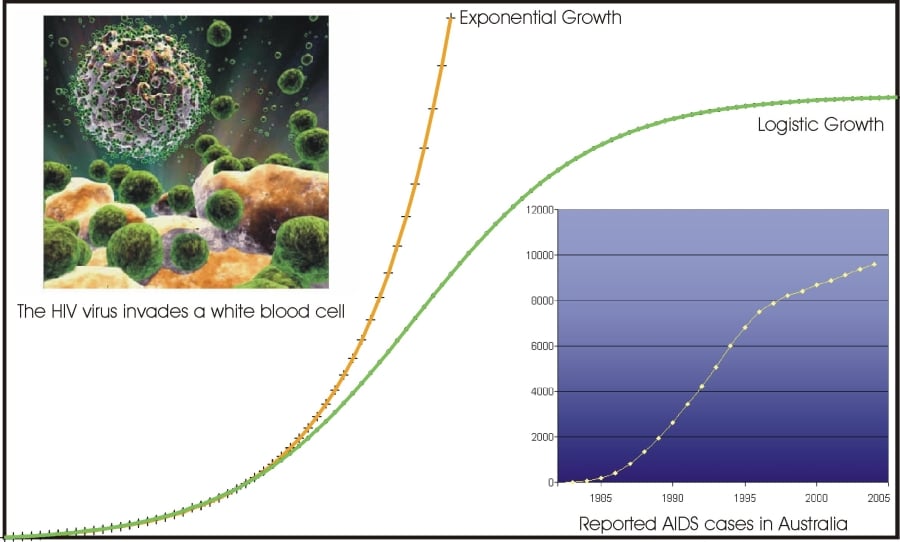
B. Modèles de développement de la résistance aux traitements

1. Modèles de résistance génétique

Les modèles de résistance génétique examinent comment les mutations génétiques dans les cellules tumorales peuvent conduire à une résistance aux traitements. Les mathématiques sont utilisées pour comprendre comment ces mutations se propagent et comment elles affectent la réponse des cellules cancéreuses aux médicaments. Cette compréhension est cruciale pour le développement de thérapies ciblées et de stratégies de traitement efficaces.

Les modèles de résistance génétique reposent souvent sur des équations différentielles pour représenter l’évolution des populations de cellules tumorales sous l’effet de la sélection naturelle due aux traitements. Voici un exemple simplifié de modèle mathématique qui illustre comment les mutations génétiques conduisent à la résistance aux traitements :

Soit N(t) le nombre de cellules sensibles au traitement à un temps t, et R(t) le nombre de cellules résistantes au traitement à ce même temps. Supposons que la croissance des cellules sensibles suit un modèle de croissance logistique et que la croissance des cellules résistantes suit également un modèle de croissance logistique, mais avec un taux de croissance plus élevé en raison de leur résistance au traitement. Nous pouvons alors modéliser cela comme suit :

1. Évolution des cellules sensibles :

\frac{dN}{dt} = rN \left(1 - \frac{N + R}{K} \right) - dN

Où :

• r est le taux de croissance intrinsèque des cellules sensibles.
• K est la capacité de charge de l’environnement (capacité maximale de support des cellules).
• dN est le taux de mortalité des cellules sensibles.

2. Évolution des cellules résistantes :

\frac{dR}{dt} = \alpha r R \left(1 - \frac{N + R}{K} \right) - dR

Où :

• α est un coefficient qui représente le facteur de résistance, généralement supérieur à 1.
• Les autres termes ont la même signification que pour les cellules sensibles.

2. Modèles de résistance induite par le microenvironnement tumoral

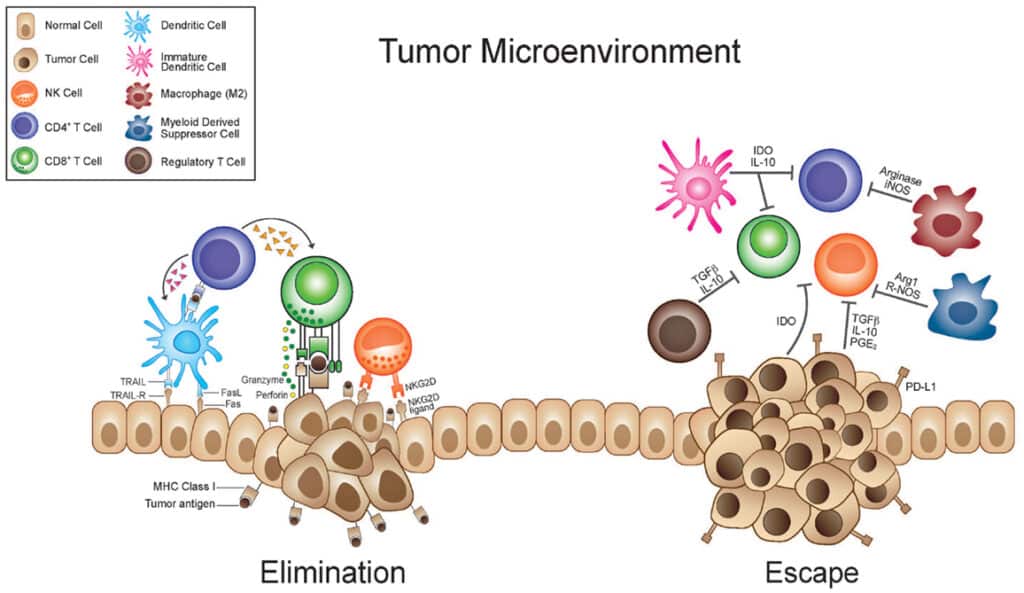
Le microenvironnement autour de la tumeur joue également un rôle important dans le développement de la résistance aux traitements. Les cellules cancéreuses peuvent modifier leur environnement pour favoriser leur survie et leur croissance malgré les tentatives de traitement. Les mathématiques permettent de modéliser ces interactions complexes entre les cellules tumorales, les cellules saines et les facteurs environnementaux, fournissant ainsi des informations cruciales pour concevoir des thérapies plus efficaces.

En étudiant ces modèles mathématiques, les chercheurs peuvent mieux comprendre la dynamique complexe des tumeurs cancéreuses et développer des stratégies de traitement plus précises et efficaces. La combinaison de la biologie et des mathématiques ouvre de nouvelles perspectives passionnantes dans la lutte contre le cancer, offrant ainsi de l’espoir à de nombreux patients et professionnels de la santé.

II. Optimisation des traitements

A. Modèles de pharmacocinétique

1. Modélisation de l’absorption, de la distribution, du métabolisme et de l’élimination des médicaments