Le paradoxe de Monty Hall
Aujourd’hui au menu, un sujet de grand oral de maths sur le problème de Monty Hall 😋

Introduction
A. Brève présentation du sujet
Le paradoxe de Monty Hall est un problème de probabilités qui tire son nom du jeu télévisé américain « Let’s Make a Deal » animé par Monty Hall dans les années 1960 et 1970. Ce problème, bien que très simple en apparence, suscite souvent confusion et débat parmi les personnes qui y sont confrontées. Derrière ce jeu, repose en réalité des principes de probabilité intéressants qui défient souvent l’intuition humaine.
B. Description du jeu et des règles
Dans ce jeu, il y a trois portes, derrière l’une desquelles se trouve un prix (disons une superbe voiture) et derrière les deux autres se trouvent des chèvres. Vous, en tant que joueur, choisissez initialement une porte, sans savoir ce qu’il y a derrière. L’hôte du jeu (le présentateur du jeu télévisé), connaissant l’emplacement du prix, ouvre ensuite une des deux portes restantes qui ne contient pas le prix. Cela crée une nouvelle information pour le joueur, qui peut choisir de modifier ou de maintenir son choix initial.
C. Démonstration d’un exemple de jeu
Supposons que vous choisissez initialement la porte numéro 1. L’hôte, qui sait où se trouve la voiture, ouvre ensuite la porte numéro 3, derrière laquelle se trouve une chèvre. À ce stade, vous avez le choix de rester avec votre porte initiale (la porte numéro 1) ou de changer pour la porte numéro 2. Le joueur peut donc adapter son choix selon sa stratégie ! (et les maths sont pour cela très utiles, eh oui ça sert parfois ce que vous apprenez en classe)
- Vous choisissez initialement une des trois portes (sans savoir ce qui se trouve derrière, en sachant qu’il y a un prix à gagner derrière l’une d’entre elles).
- L’hôte du jeu, qui sait ce qui se cache derrière chaque porte, ouvre une des deux portes que vous n’avez pas choisies, révélant une porte sans prix.
- À ce stade, vous avez la possibilité de rester sur votre choix initial ou de changer de porte.
- Une fois que vous avez pris votre décision, la porte sélectionnée est ouverte, et vous découvrez si vous avez gagné le prix ou non.
I. Analyse intuitive du problème
A. Un problème, deux points de vues
Ce jeu va à l’encontre de ce que l’on pourrait penser, car la plupart des gens voient les choses de deux façons différentes :
Certains disent qu’après que l’hôte a ouvert une porte, il reste deux portes, donc les chances sont de 1 sur 2 de gagner, que l’on garde sa porte ou qu’on en choisisse une autre. Grossomodo, ça revient au même, que tu changes de porte ou pas.
D’autres pensent que si tu gardes ta porte initiale, tu ne gagnes que si tu avais choisi la bonne porte dès le départ, ce qui n’était qu’une chance sur trois. Donc, ça revient à dire qu’il y a 1 chance sur 3 de gagner sans changer de porte, et 2 chances sur 3 de gagner en changeant.
B. Le point de vue correcte
Ces affirmations contradictoires ont donné naissance à un paradoxe. En réalité, si le participant décide de changer de porte, ses chances de remporter la voiture passent de 1/3 à 2/3, tandis que ses chances de gagner en restant avec son choix initial demeurent à 1/3. Bien que cela puisse sembler contre-intuitif, la meilleure stratégie est donc de toujours changer de porte. C’est ce que nous allons maintenant examiner en résolvant ce problème.
II. Approche probabiliste
A. Formulation du problème en termes de probabilités
La solution repose sur trois cas que nous allons numérotés et définir en fonction du choix initial :
- Cas 1 (noté C1) : Si le candidat choisit initialement la porte de la chèvre 1 et que le présentateur ouvre la porte de la chèvre 2, alors la porte restante cache la voiture et le candidat gagne.
- Cas 2 (noté C2) : Si le candidat choisit initialement la porte de la chèvre 2 et que le présentateur ouvre la porte de la chèvre 1, alors la porte restante cache la voiture et le candidat gagne.
- Cas 3 (noté C3) : Si le candidat choisit initialement la porte de la voiture et que le présentateur ouvre la porte d’une des deux chèvres, alors la porte restante cache une chèvre et le candidat ne gagne pas.
On remarque que dans 2 cas sur 3, la porte restante cache la voiture.
Soit C1, C2 et C3 les événements correspondant aux portes 1, 2 et 3 respectivement. Et G l’événement « le joueur gagne ».
Ce que nous cherchons à savoir, et s’il vaut mieux changer de choix ou non. Alors quelle est la meilleure stratégie ? Distinguons donc ces deux cas, et calculons les probabilités pour ne plus se faire avoir 😉
B. Le joueur change de porte
Effectuons une simulation du jeu en imaginant que le joueur change de porte :
- Si le candidat avait initialement choisi une porte à chèvre (C1 et C2), changer de porte le conduit toujours à gagner la voiture, soit une probabilité de 1.
- Si le candidat avait initialement choisi la porte de la voiture (C3), changer de porte le conduit toujours à ouvrir une porte à chèvre, donc une probabilité de 0. Ainsi, la probabilité de gagner en changeant de porte est de 1 * 2/3 + 0 * 1/3, ce qui équivaut à 2/3.
\begin{aligned}
P(G) &= P(G,C1)+P(G,C2)+P(G,C3) \\
&= P(G|C1)P(C1)+P(G|C2)P(C2)+P(G|C3)P(C3).
\end{aligned}Or initialement, chaque cas a autant de chance d’être choisi (on choisit une porte au hasard), donc
P(C1)=P(C2)=P(C3)=1/3.
Si l’on a initialement choisi une porte à chèvre (cas C1 et C2), changer de porte conduit à gagner la voiture donc P(G|C1) = P(G|C2) = 1. En effet, si on choisit une porte à chèvre, le présentateur va ouvrir l’autre porte à chèvre (il ne va bien évidemment pas ouvrir la porte à voiture, donc la 3ème porte restante est avec certitude la porte à voiture).
À contrario, si le joueur avait initialement choisi la porte de la voiture (cas C3), changer de porte conduit à une défaite, donc P(G|C3) = 0.
C. Le joueur ne change pas de porte
Maintenant, imaginons que le joueur ne change pas de porte :
- Dans ce cas, le candidat ne gagne que s’il avait choisi initialement la porte de la voiture, ce qui donne une probabilité de 1.
- Si le joueur ne change pas de porte, la probabilité de gagner est de 0 * 2/3 + 1 * 1/3, soit 1/3.
\begin{align*}
P(G) &= P(G,C1) + P(G,C2) + P(G,C3) \\
&= P(G|C1)P(C1) + P(G|C2)P(C2) + P(G|C3)P(C3).
\end{align*}
Si on ne change pas de porte, on ne gagne que si l’on avait initialement choisi la bonne porte donc P(G|C3)=1 et P(G|C1) = P(G|C2) = 0.
D. Conclusion
Changez de porte !! La probabilité de gagner est deux fois plus élevée en changeant de porte. Changer de porte fait passer la probabilité de repartir avec la voiture de 1/3 à 2/3 !

On ne dort pas !! Ce n’est pas encore fini…
III. Simulation et expérimentation
A. Utilisation d’un programme informatique pour simuler le jeu de Monty Hall
Pour mieux comprendre le paradoxe de Monty Hall, nous pouvons utiliser un programme informatique pour simuler le jeu de manière répétée. Cela nous permettra de recueillir des données empiriques sur les résultats du jeu et de comparer ces résultats avec les prédictions théoriques basées sur les probabilités.
Nous pouvons écrire un programme simple en Python pour simuler le jeu de Monty Hall. Voici un exemple de code :
import random
import matplotlib.pyplot as plt
def monty_hall_simulation(change_choice):
doors = [0, 0, 1] # 0 représente une chèvre, 1 représente le prix
random.shuffle(doors)
initial_choice = random.randint(0, 2)
opened_door = next(i for i in range(3) if i != initial_choice and doors[i] == 0)
if change_choice:
final_choice = next(i for i in range(3) if i != initial_choice and i != opened_door)
else:
final_choice = initial_choice
return doors[final_choice] == 1
def run_simulation(num_trials):
wins_change = 0
wins_keep = 0
win_percentage_change = []
win_percentage_keep = []
for _ in range(num_trials):
if monty_hall_simulation(True):
wins_change += 1
win_percentage_change.append(wins_change / (_ + 1))
if monty_hall_simulation(False):
wins_keep += 1
win_percentage_keep.append(wins_keep / (_ + 1))
return win_percentage_change, win_percentage_keep
def plot_results(win_percentage_change, win_percentage_keep):
plt.plot(range(1, len(win_percentage_change) + 1), win_percentage_change, label="Changer de porte")
plt.plot(range(1, len(win_percentage_keep) + 1), win_percentage_keep, label="Garder la porte")
plt.xlabel("Nombre de tentatives")
plt.ylabel("Pourcentage de victoires")
plt.title("Comparaison du jeu de Monty Hall")
plt.legend()
plt.show()
# Exemple d'utilisation
num_trials = 1000
win_percentage_change, win_percentage_keep = run_simulation(num_trials)
plot_results(win_percentage_change, win_percentage_keep)
B. Présentation des résultats de la simulation
Après avoir exécuté la simulation un grand nombre de fois, nous pouvons compiler les résultats pour obtenir des statistiques sur les performances du joueur en gardant ou en changeant de choix.
Comme on est sympa, on l’a fait à votre place 🔥.
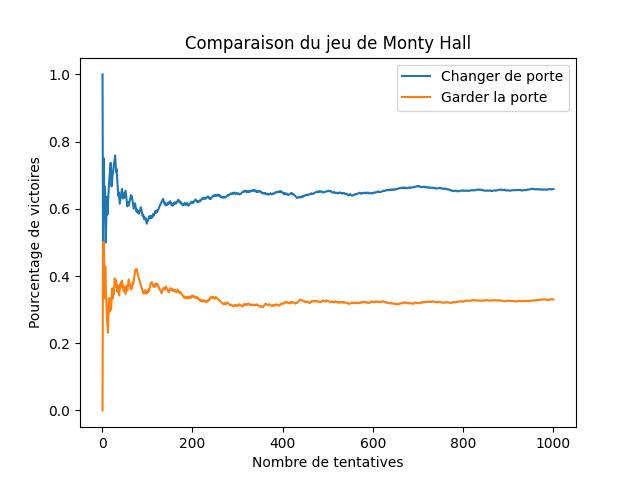
Ce graphe confirme bien qu’on ne disait pas n’importe quoi 💪
On voit bien que la probabilité de gagner en changeant de porte est plus élevée (environ 2 fois plus) que celle en conservant son choix initial.
Retenez aussi que plus on fait de tentatives, plus le résultat expérimental se rapproche de la probabilité théorique.
C. Comparaison avec les résultats théoriques
En comparant les résultats de la simulation avec les prédictions théoriques que nous avons calculées précédemment, nous observons bien une concordance significative (surtout avec un grand nombre de tentatives). Cela renforce donc notre compréhension du paradoxe de Monty Hall et démontre l’importance des probabilités dans la prise de décision stratégique lors de ce jeu.
Conclusion
A. Récap des principaux points abordés
Dans cet exposé, nous avons examiné en détail le célèbre paradoxe de Monty Hall. Nous avons commencé par présenter le jeu et énoncer le problème, puis nous avons exploré les différentes perspectives et intuitions qui émergent de ce jeu.
B. Mise en avant de l’importance de la stratégie dans le paradoxe de Monty Hall
Nous avons clairement démontré que la stratégie adoptée par le joueur joue un rôle crucial dans ses chances de gagner. En analysant les probabilités et en réalisant des simulations, nous avons montré que changer de porte après l’ouverture d’une porte non gagnante par l’hôte offre en réalité une probabilité de gain plus élevée, contrairement à ce que l’intuition initiale pourrait suggérer.
C. Ouverture sur d’autres problèmes similaires ou applications dans d’autres domaines
Le paradoxe de Monty Hall n’est qu’un exemple fascinant parmi de nombreux autres problèmes et paradoxes intéressants en probabilités et en théorie des jeux. En explorant ces concepts, nous pouvons développer notre compréhension des probabilités et de leur application dans divers domaines, tels que l’économie comportementale, la sécurité informatique et même la prise de décision dans la vie quotidienne.
Le problème de Monty Hall nous enseigne non seulement sur les subtilités des probabilités, mais aussi sur l’importance de remettre en question nos intuitions et d’adopter une approche stratégique et analytique dans la résolution de problèmes complexes.
Questions et débats (préparation à l’entretien !)
A. Invitation du public à poser des questions
Je vous invite maintenant à poser vos questions sur le paradoxe de Monty Hall ou sur tout autre sujet lié aux probabilités et aux jeux de décision, et je vais essayer d’y répondre.
B. Discussion sur les implications du paradoxe de Monty Hall
Le paradoxe de Monty Hall met en évidence des concepts fondamentaux de la théorie des probabilités et de la prise de décision. En discutant de ses implications, nous pouvons explorer plusieurs idées intéressantes :
- L’importance de la stratégie dans les jeux de hasard : Le paradoxe de Monty Hall montre comment une stratégie de changement peut considérablement augmenter les chances de succès, même lorsque les probabilités semblent contre-intuitives.
- La nature de l’information et de la prise de décision : L’effet de l’information révélée par l’hôte dans le jeu de Monty Hall soulève des questions sur la façon dont les individus traitent et utilisent l’information dans la prise de décision.
- Les applications dans d’autres domaines : Les principes sous-jacents au paradoxe de Monty Hall sont pertinents dans de nombreux autres contextes, tels que l’économie comportementale, la théorie des jeux et la sécurité informatique.
C. Échange sur d’autres énigmes ou paradoxes intéressants en probabilités
En plus du paradoxe de Monty Hall, il existe de nombreuses autres énigmes et paradoxes fascinants en probabilités. Voici quelques exemples que nous pourrions explorer ensemble :
- Le paradoxe des anniversaires : Il s’agit d’une question sur la probabilité que, dans un groupe donné de personnes, au moins deux d’entre elles aient la même date d’anniversaire.
- Le paradoxe des deux enfants : Ce paradoxe implique de déterminer la probabilité que les deux enfants d’une famille soient de même sexe, sachant qu’au moins l’un d’eux est une fille.
- Le problème de la marche aléatoire : Ce problème explore la probabilité de revenir à un point de départ après un certain nombre d’étapes dans une marche aléatoire sur un réseau discret.
En discutant de ces énigmes et paradoxes, nous pouvons approfondir notre compréhension des concepts probabilistes et leur pertinence dans différents contextes de la vie réelle.



